4.1 Primes

A prime number is a number greater than 1 which is only divisible by itself and 1. The first primes are 2, 3, 5, 7, 11, and so on. Earlier it was stated that there are infinitely many primes. This was proved by Euclid around 300 BC. Once again, it initially seems counterintuitive that the primes should carry on forever. As numbers get bigger there are more potential divisors, so you might think there’s eventually a point where primes just stop. Here you will look at one proof that there are indeed infinitely many primes.

The first thing you need to know is that every number can be written as the product of ‘prime divisors’. Either it’s a prime, and therefore is its own prime divisor, or it isn’t prime, and it can be broken up and written as the sum of its primes (prime 1 x prime 2 x …). The second important fact is that this prime factorisation is unique to each number. This bold-sounding statement isn’t all that difficult to prove, but it’s a little beyond the scope of this course. Here are a couple of examples to demonstrate the idea:

15 = 3 x 5

There are no other prime numbers you can multiply together to make 15. You can use the same primes more times to get different prime factorisations:

75 = 3 x 5 x 5

Try this out for yourself.

Once you’re happy that any number can be written uniquely as the product of primes, you can look at how to prove there are infinitely many primes. You use something call ‘proof by contradiction’. You can argue by instead assuming the opposite of the claim, and showing this leads us to an impossible conclusion. In mathematics, if you go through a series of steps which takes you to a contradiction, you know there is something wrong with an earlier step. There are no contradictions allowed in mathematics.

To prove there are infinitely many primes, then, you first assume the opposite – that there are finitely many primes – and you start by listing them. To make this proof easier to picture, label the primes p₁, p₂ , p₃, p₄ and so on, all the way up to the ‘last’ prime. So p₁ = 2, p₂ = 3, p₃ = 5, p₄ = 7, and as we don’t know how big our last prime is, we just use a letter to stand for it, so that’s p_r.

Now, think about the number you get when you multiply the whole list of primes together and add 1.

It may take a minute to believe it, but none of the primes in our list can divide this number. Each one leaves a remainder of 1. Now, every number can be written uniquely as a product of primes, so there must be some prime that’s not in our list which divides the result above. It’s not one of the primes in our list, and that list supposedly contained all primes. This shows that the assumption that there was a finite list of primes was false. Therefore, there are infinitely many primes.

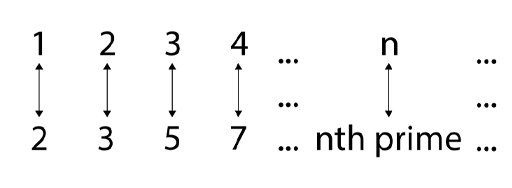
To confirm that there are as many primes as there are counting numbers, you first observe that all the primes are contained in the counting numbers, so it’s not a bigger infinite set than the counting numbers. To give a mapping to the counting numbers (a pairing between all the counting numbers and primes) you simply enumerate the primes: first prime, second prime, third prime and so on. As before, this shows that each set of numbers has the same size.

Show description|Hide description

This is a diagram of the numbers 1 to 4 followed by an ellipsis, then the letter n followed by an ellipsis. The first row of numbers is above a second row of prime numbers (2, 3, 5, 7) followed by an ellipsis and the expression ‘nth prime’. An arrow is joining each number on the top row with a single prime number on the bottom row.

This is a powerful piece of information. The fact that there are infinitely many primes forms the base of a great deal of cryptography, as staggeringly large primes are used to protect data. Finding larger and larger primes is hard and can use complex theories. We don’t actually know what all the prime numbers are, and the next prime can’t currently be predicted, which is part of the security of using prime numbers.

There is an open problem in mathematics called the Riemann hypothesis. If this were proved, then we could predict how the prime numbers are distributed (but it still won’t tell us which the next prime number is!). In fact, proving the Riemann hypothesis is one of the Millennium Prize Problems, a set of important unsolved mathematical problems which each carry a million-dollar prize.