4.2 Fractions
It was stated earlier that there are as many fractions as counting numbers. At face value, this is even harder to swallow than the matching between the even numbers and the counting numbers. Between any two whole numbers there are infinitely many fractions. This is because between any two numbers (fractions or whole numbers) there is another fraction. No matter how small the gap between any two fractions, there is always another one in between.
Think about the gap between 0 and 1/2. There is another fraction halfway between them, 1/4. Then you can find the point in the middle of these fractions. Now you’ve added in 1/8 and 3/8. You can keep adding points in the middle of the fractions you already have, and you’ll never reach an end.
Because the fractions are densely packed in this way, you might think there would be ‘more’ of them than the counting numbers. So, how can you give a matching between the fractions and the counting numbers?
Here you will just look at the positive numbers and the positive fractions. Cantor argued this in the following way. First, lay out all the fractions in a grid. A fraction is any number divided by another number. The grid is constructed so that the first row has one over every number, the second row has two over every number, and so on. The first column is every number over one, the second column is every number over two, and so on. The first part of the argument is to realise that every fraction will appear somewhere in this grid.
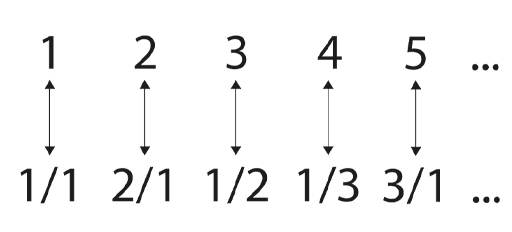
The matching between the fractions and the counting numbers is then given by the diagonal ‘walk’ shown in Figure 7. Simply match 1 with the first step in the walk, match 2 with the second step, etc. Every fraction will be visited. Occasionally you’ll hit a number which is a repeat of what you had before. Skip over these and continue with your matching.
Following the diagonal walk gives a mapping between the counting numbers and the fractions, confirming that the set of fractions is the same size as the set of counting numbers.
There are bigger infinite sets of numbers. As stated earlier, once you include the numbers which cannot be written as fractions, the ‘irrationals’, you can no longer make a matching between these numbers and the counting numbers. Sets of this size are called ‘uncountable’. Cantor’s proof of this again uses a diagonal argument. This time he uses the technique ‘proof by contradiction’, just as you did with the proof that there are infinitely many primes. This proof starts by assuming that the set of irrationals can be counted – and it reaches a contradiction. This shows that the set of irrationals cannot be mapped to the counting numbers and is therefore uncountable. So, infinite sets can be different sizes!
It was said earlier that you can ‘count’ infinite sets by matching/pairing them with the counting numbers. Similarly, you can compare sizes of infinite sets by finding a matching/pairing between the members of those sets. There are other mathematical techniques for comparing the sizes of infinite sets as well.
It turns out that whatever infinite set you have, you can make a genuinely bigger one out of it. This means there is no ‘biggest’ size of infinity.