6 The paradox of fractals
Fractals are beautiful objects that combine ideas of the infinitely big, the infinitely small, dimensions of space and practical real-world applications. Here are a few examples.

Fractals are objects which contain copies of themselves. They appear similar at all levels of magnification. It’s sort of like Doctor Who’s TARDIS being ‘bigger on the inside’, but in this case each TARDIS has another TARDIS inside. Or you could think of them like nesting Russian dolls that go on forever.
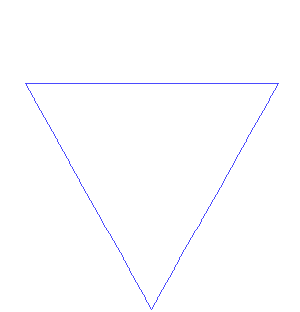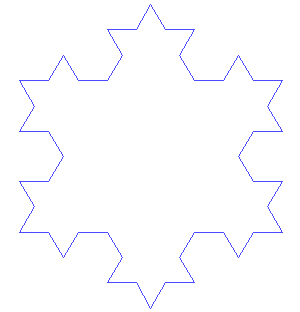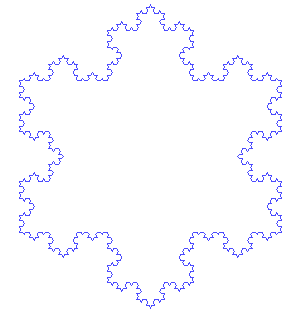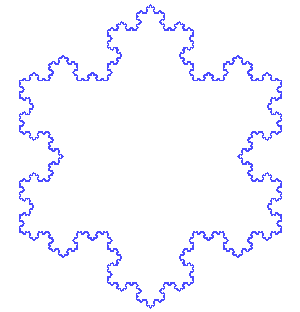
One relatively simple fractal is the Koch snowflake, displayed in Figure 12. A Koch snowflake is obtained by taking an equilateral triangle and removing the middle third of each edge and replacing it with a smaller equilateral triangle. You repeat the process with the resulting shape. You remove the middle third of each edge and replace it with an equilateral triangle. This process is repeated and repeated. The Koch snowflake is the mathematical object you have after infinitely many repetitions.
It has a finite area. You can show this by enclosing it in a finite circle (or any other shape). But its perimeter is infinite. It’s infinitely ‘wiggly’. Here is where mathematics gets really mind-bending, as the boundary is said to have a ‘fractional dimension’, which works differently than the 1-dimensional or 2-dimensional description you might expect for a flat object (it actually has a dimension of 1.26 in this case). Fractals are an interesting subject in their own right – one that quickly becomes mathematically complex and counter-intuitive.
Another relatively simple fractal to describe is the Sierpinski triangle, seen in Figure 13. To make a Sierpinski triangle, you start the first stage with a solid shaded equilateral triangle. At the second stage, you split the triangle into four equal equilateral triangles and remove the middle triangle. At the third stage, you split the three remaining shaded triangles into four equal equilateral triangles each and remove the middle triangles. The final object is made once this process has run infinitely.
Activity 2 The making of a Sierpinski triangle
Using the information above, see if you can complete this table with the number of triangles at each stage.
| Stage | Number of shaded triangles |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | |
| 4 | |
| 5 |
How many shaded triangles will there be at the nth stage?
(Hint: note that at stage 2, you have 31. At stage 3, you have 32. Now check the other stages in terms of powers of three.)
Answer
The answer is 3n-1.
Apart from giving rise to attractive images, the fractal process was a game changer in the animation industry. Before the advent of this process, animations were somewhat flat and incredibly laborious. Loren Carpenter realised he could use the fractal process to give any desired level of complexity to the images in his animations. The process is used to make surfaces have texture, as you can see in Video 4. This work revolutionised animated film.