1.2 Pascal’s triangle – a closer look
As well as the patterns within the triangle being interesting in their own right, they are used in maths and science. If you continue your study at university level in these areas you may well come across Pascal’s triangle and will already be prepared for its delights. Also, having a go at spotting the patterns now will give you a chance to practise your pattern-spotting skills and you may well be surprised by how many there are!
Activity 3 Identifying patterns
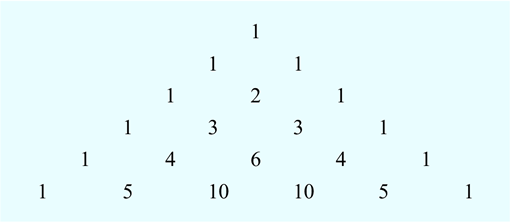
Study this six-row version of Pascal’s triangle and note down any patterns that you can spot.
Click on ‘reveal comment’ for tips on how to get started.
Comment
Play around with the numbers to find patterns. Try looking down the diagonals and adding the numbers in each row.
Answer
- Each row starts and ends with a 1.
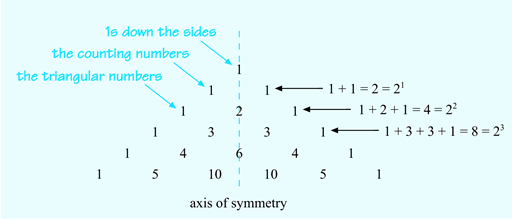
- The counting numbers, 1, 2, 3, 4, 5, are in the diagonal rows next to the sides.
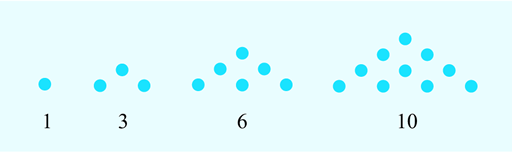
- In the next diagonal row, there is the sequence 1, 3, 6, 10. These numbers are known as the ‘triangular numbers’ because they create triangular patterns as shown in Figure 5:
- Pascal’s triangle is symmetrical, too. If you draw a vertical line down through 1, 2, 6, one side of the triangle is a mirror image of the other.
- The sums of the first six rows are 1, 2, 4, 8, 16, 32. The total for the next row is double the total for the current row.
These numbers can also be written as 1, 21, 22, 23, 24 and 25.
The pattern in the powers of 2 shown in Figure 6 suggests that the first total, 1, might be written as 20. Check on your calculator to see if this is correct. So it can also be said that the sums of each row are square numbers and these can be generated by raising 2 to the row number minus 1. Figure 6 may help you to see this more clearly than a written description:
Well done if you spotted some or all of those patterns. There are many more than those looked at here, so this is just a flavour of what can be found in Pascal’s triangle.
What do the two examples have to do with mathematics? Well, recognising patterns in shapes, sets of numbers, processes or problems, and noticing what is the same and what is different about situations, often makes a task easier to solve. You saw how recognising the tiling pattern in Activity 1 made it easier to remember and describe, and by using the number patterns in Pascal’s triangle, you could work out the sum of each row without adding the individual numbers.
If you can spot a pattern and then describe what happens in general, this can lead to a rule or formula. If you can prove that this rule will always work, it can be used elsewhere. For example, if you can work out the general process for calculating a quarterly electricity bill and then give these instructions to a computer, many electricity bills can be generated, printed and sent out in just a few minutes. It may also help you to understand your bill!
In the next section you will start to look at how this process of looking for relationships can be used to write rules.