2 Looking for relationships
This section considers the relationship between quantities in two practical situations and shows you how to describe these relationships by writing down a general rule or a word formula. You can think of these as a set of mathematical instructions. A good way to start is to use an everyday example.
Suppose you are planning a visit abroad. Your map marks all the distances between places in kilometres rather than miles, which you are used to dealing with. How can you work out what these distances are in miles? The first type of information you will need is how long one kilometre is, measured in miles. If you want to, you could use the internet to verify that 1 km is equivalent to approximately 0.6214 miles.
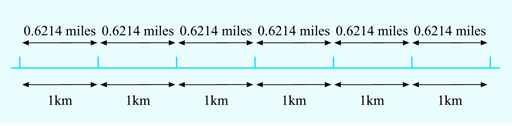
The next step is to work out how, using maths operations, you would convert kilometres into miles. You may be able to see how to convert from kilometres into miles immediately from your study of weeks 1 and 2 of this course – but, if not, try to visualise a few simple examples. The diagram in Figure 7 should help with this, as it shows how kilometres relate to miles:
So if the distance is 3 km, you will have 0.6214 miles three times; if the distance is 10 km, you will have 0.6214 miles 10 times; if the distance is 250 km, you will have 0.6214 miles 250 times, and so on.
You can write this last example down mathematically as:
(to the nearest whole number)
Notice that in each of the examples above, the process for calculating the number of miles was the same: multiply the number of kilometres by 0.6214 (the conversion factor). This technique will work for any distance, and so the following word formula can be written:
Note that what the word formula works out is stated first – this is the standard way of presenting any formula.
You can use this formula to convert any distance in kilometres into miles. For example, suppose you wanted to convert 500 km, using the formula and replacing ‘distance in kilometres’ with 500 gives:
So 500 km, rounded to the nearest whole number, is equivalent to 311 miles.
In this example, you used the formula by replacing the phrase ‘distance in kilometres’ on the right side of the equation by the corresponding value, 500. This is known mathematically as substituting the value into the formula.
Have a go at this yourself in our next activity.
Activity 4 How many miles?
Using the word formula just worked out, calculate how far 350 km is in miles. Show your answer to the nearest mile.
Answer
Substituting 350 for ‘distance in km’ gives:
So, 350 km is approximately 217 miles to the nearest mile.
Now that you have used a word formula, you can move on to finding your own word formula in an activity with a similar idea behind it. Remember that drawing diagrams can help you with spotting relationships and patterns!