1.2 Is the mean the best average to use?
As you learned earlier one of the advantages of using the mean as an average value is that it takes account of all the values in the data set. However, this also means that if one of the values is much higher or lower than the other values it can greatly affect the mean. The following activities will look at this.
Suppose somebody is planning a visit to Vermont, USA in October and they want an idea of how much rainfall there will be. To do this they consult records from the National Climate Data Center in the USA, and find the following:
| Year | 2007 | 2008 | 2009 | 2010 | 2011 |
|---|---|---|---|---|---|
| Rainfall, in inches (to 1 d.p.) | 5.8 | 5.2 | 4.6 | 9.3 | 4.5 |
What the person really wants to know though is, is what the typical value for October would be. Let’s start with calculating the mean to find this.
Activity 2 How wet is it in Vermont in October?
Find the mean rainfall in Vermont in October for these five years.
Answer
Over these five years the mean rainfall was 5.9 inches (to 1 decimal place).
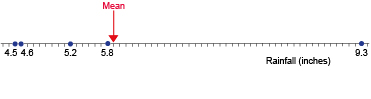
Now look at the five data values again. Does 5.9 inches give you a good idea of how much rainfall there has been? One way to look at this is using a number line, with all the data values plotted on it, as shown below in Figure 1:
This shows that, in four out of the five years, rainfall was below the mean, while it was above the mean in only one year. In that year, the rainfall was particularly high and this has pulled the mean up. So the mean is perhaps not a particularly good choice for a typical value in this case. So let’s see if a different average would be better – this time the median.