1.3.5 The benefit to savers of compound interest
The calculation of interest on savings accounts is straightforward. Interest accrues at a rate based on the savings rate and the balance of money in a savings account. So if £1000 is held in an account where the rate is 5% per annum then interest paid at the end of the year is £1000×5/100=£50.
In many cases, with movements into and out of savings accounts taking place, the interest charged will be based on the average balance of the principal sum during the year. For instance, if £10,000 is invested at the start of the year and £100 is withdrawn halfway through each month, then the outstanding balance at the end of the year would be £8800. The average balance of principal outstanding during the year would be the average (mean) of the balance at the start and at the end of the year, or (£10,000+£8800)/2=£9400. Based on this average balance, the interest for the year at 5% p.a. would be £9400×5/100=£470 – less than the £500 that would have been received if no withdrawals had been made.
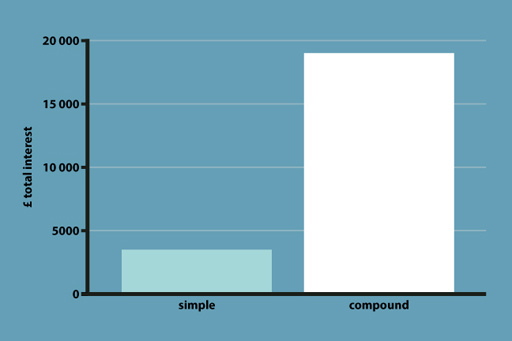
What happens if the lender does not withdraw the interest received and adds it to the balance of the account? This would mean that the following period’s interest earnings is going to be higher since the borrower will be paying interest, not only on the original principal sum but also on the re-invested interest. This is known as compounding, and can quickly enlarge savings during periods of high interest rates.
Consider what happens if someone lends £1000 at an interest rate of 3.5% and makes no withdrawals over ten years. Over this period of time, the investment would rise from £1000 to £1411 (£411 interest on top of the £1000 invested). This is more than if interest had been charged on a simple rather than compound basis – simple interest over ten years would have been just £350.
You can test this out for yourself, using our interest calculator [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] .
The precise practice for computing the interest earnings varies among different borrowers – and interest can be calculated at different time intervals. One of the pieces of financial small print it is always vital to read is the basis on which interest is paid – that is, how often and by reference to what terms.