1.2 Inductive reasoning and reasoning by analogy
1.2.1 Inductive reasoning
Inductive reasoning involves drawing a general conclusion from specific examples. When inductive reasoning takes place, the process is generally the reverse of deductive reasoning. It involves finding out the name of the wider category A of things that correctly describes all of the observable objects in that category. This can then be used to say something new about the specific case C that you are dealing with at the time. It is done by observing what you already know from a number of existing examples, collecting that knowledge together and forming a general rule about all of those examples that should also apply to other examples in the same category.
It is rarely possible, for example, to observe all possible instances of something. Therefore a general conclusion based on some specific instances that purports to account for all instances will not always or necessarily be true. It will only probably be true based on the available evidence. Look at this example, which might come up if you were wandering around ancient Greece:
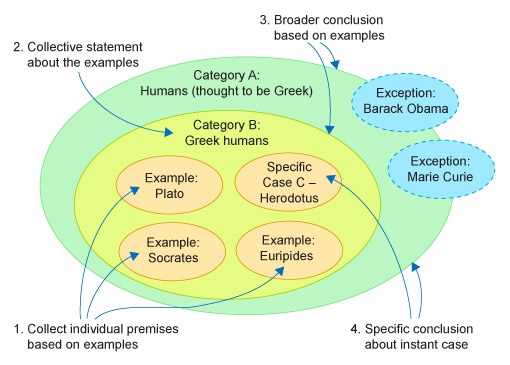
| Step 1 | Observe examples: This human Socrates is Greek. And this human Plato is Greek. And this human Euripides is Greek. |
| Step 2 (hidden step) | Collect them together based on shared characteristics. |
| Step 3 | Broader conclusion based on Step 2: Therefore all humans (category B) are Greek (category A). |
| Step 4 | Apply to specific case: Therefore this other human Herodotus (case C) is also Greek (category A). |
If you happen to see only Greek men, then you might logically but incorrectly conclude that all humans are Greek. (You might also incorrectly conclude that all humans are men.) The logical relationship between the statement categories is consequently less certain than with deductive reasoning, and is illustrated in Figure 3.
In this example, as you have not been made aware of the existence of Barack Obama or Marie Curie from your experience, you have received incomplete information about the nationality of humans, which has resulted in a discrepancy in the general rule you have constructed from that information, that all humans are Greek. As Figure 3 illustrates, there is no necessary connection between those in the category of Greek humans and those in the broader category of humans. If you then use deductive reasoning to apply a flawed general principle derived from inductive reasoning to a specific case, you may end up with a statement about the case that is not true. It happened to be true that Herodotus was Greek, but if your case had been Marie Curie, this conclusion would not be true as she was French-Polish.
Inductive reasoning is not as rigorous as deductive reasoning in terms of its logical process. Instead, it is the process of building a hypothesis, a theory about a general rule, from the evidence available that both supports that theory and contradicts competing theories. The more evidence there is available, the higher the probability that the conclusion, the general rule, will be correct, but this can never be known for certain.