2 Large quantities and small quantities – scientific notation
Scientists frequently deal with enormous quantities – and with tiny ones. For example, it is estimated that the Earth came into being about four and a half thousand million years ago. It took another six hundred million years for the first living things – bacteria – to appear. Bacteria are so small that they bear roughly the same proportion to the size of a pinhead as the size that pinhead bears to the height of a four-year old child!
Powers of ten provide a convenient way of writing down very large or very small numbers. For example,
106 = 1 000 000 (a million) and 10−3 = 1/1000 = 0.001 (a thousandth)
This shorthand can be extended to any quantity, simply by multiplying the power of ten by a small number. For instance,
2 × 106 = 2 × 1 000 000 = 2 000 000 (two million)
(The quantity on the left-hand side would be said as ‘two times ten to the six’.) Similarly,
3.5 × 106 = 3 500 000 (three and a half million)
7 × 10−3 = 7/1000 = 0.007 (seven thousandths)
Scientists make so much use of this particular shorthand that it has come to be known as scientific notation (although in maths texts you may also find it referred to as ‘standard index form’ or ‘standard form’).
A quantity is said to be expressed in scientific notation if its value is written as a number multiplied by a power of ten. The number can be a single digit or a decimal number, but must be greater than or equal to 1 and less than 10.
Note the restriction: 75 × 102 is not in scientific notation and nor is 0.75 × 104, though these are both equivalent to 7.5 × 103 which is in scientific notation.
Scientific notation can be defined more succinctly by making use of some of the mathematical symbols denoting the relative sizes of quantities. These symbols are:
| > | greater than (e.g. 3 > 2); |
| ≥ | greater than or equal to (e.g. a ≥ 4 means that the quantity a may take the exact value 4 or any value larger than 4); |
| < | less than; |
| ≤ | less than or equal to. |
Note that:
- a≥ 4, and
- 4 ≤ a
convey exactly the same information about the quantity a.
Using these symbols, scientific notation may be defined as a notation in which the value of a quantity is written in the form a × 10n, where n is an integer and 1 ≤ a < 10.
To move from scientific notation to integers or to decimal notation, first deal with the power of ten, then carry out the multiplication or division.
Look at this worked example and then have a go at the questions that follow yourself.
Worked example 1
Express the following numbers as integers or in decimal notation:
- a.4.53 × 103 = 4.53 × 1000 = 4530
- b.8.371 × 102
- c.6.4 × 10−3
Answer
- a.
- b.
- c.
Note that, as in Worked example 1, a requirement to express a quantity in a different form simply involves taking the quantity and writing down its equivalent in the new form. You may do this in one step, or write down intermediate steps as was done in the worked example.
Now try this in the following activity.
Activity 2 Scientific notation to integers or decimal notation
Without using your calculator, express the following numbers as integers or in decimal notation. Note that (a) and (b) are in scientific notation, while (c) is not.
- a.5.4 × 104
- b.2.1 × 10−2
- c.0.6 × 10−1
Answer
- a.
- b.
- c.
Moving from an integer or decimal notation to scientific notation is equivalent to deciding what power of ten you need to multiply or divide by in order to convert the number you are starting with to a number that lies between 1 and 10. The following worked example shows you how to carry this out.
Worked example 2
Express the following numbers in scientific notation:
- a.356 000
- b.49.7 × 104
- c.0.831
Answer
- a.
- b.
- c.
In this worked example, all the steps have been written out in full. You may be able to manage with fewer steps in your own calculations - just use as many or as few as you feel comfortable with in order to get the right answer!
Now try this in the following activity.
Activity 3 An integer or decimal notation to scientific notation
Without using your calculator, express the following numbers in scientific notation:
- a.215
- b.46.7
- c.152 × 103
- d.0.0000876
Answer
- a.
- b.
- c.
- d.
Another way to work out how to express numbers in scientific notation is to count how many positions you move the decimal point to help you find the power of 10. Moving it to the left increases the power of 10 by one for each position moved, while moving it to the right decreases the power of 10 by one for each position moved.
So, other possible solutions are:
(a) 215 can be written as 215. that is with the decimal point after the 5. To change to scientific notation, you have to move it 2 places to the left, and this gives 10 to the power +2, and hence 2.15 × 102.
Similarly for (c) 152. × 103 (writing in the decimal point). It has to move 2 places to the left to be behind the first non-zero digit, the 2, and so the power of 10 increases by 2 to give 1.52 × 105.
In (d) you have to move the decimal point to the right, and this decreases the power of 10, so making it a negative number here. It has to move 5 places left to be behind the first non-zero digit, the 8, and so we get 8.76 × 10–5.
It is only too easy to lose track of the sizes of things when using scientific notation, so you should make a habit of thinking carefully about what the numbers mean, bearing in mind that numbers may be positive or negative. For example:
- −1 × 1010 is a very large negative number;
- −1 × 10−10 is a very small negative number;
- 1 × 10−10 is a very small positive number.
Figure 1 places on the number line some numbers in scientific notation. You may find this helps you to visualise things.
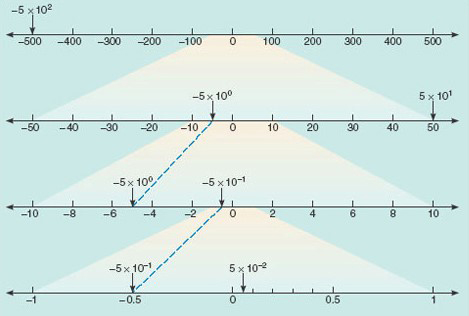
You started this section thinking about the early Earth and the first appearance of life. Using scientific notation, the age of the Earth can be neatly expressed as 4.6 × 109 years and the size of one type of those early bacteria as 1.2 × 10−6 metres. Of course, the value you come up with for such sizes will depend on the units in which we choose to make the measurements. If you were measuring the diameter of the Moon, you could elect to express it in metres or in kilometres, or even in miles.
Units of measurement will be covered next week. Before moving on to that it’s time to attempt the first short quiz.
