4 How precise are the measurements?
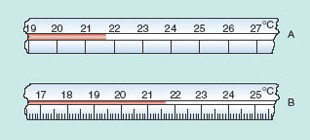
Scientists and technologists are always trying to get better and more reliable data. One way of getting a more precise measurement might be to switch to an instrument with a more finely divided scale. Figure 4 shows parts of two thermometers placed side by side to record the air temperature in a room.
The scale on thermometer A is quite coarse. The marked divisions represent integer numbers of degrees. On this scale you can see that the temperature is between 21 °C and 22 °C. You might estimate it as 21.7 °C, but somebody else could easily record it as 21.6 °C or 21.8 °C. So there is uncertainty in the first decimal place, and no way you could attempt to guess the temperature to two decimal places using this particular thermometer.
Thermometer B has a finer scale, with divisions marked every 0.1 °C. Now you can clearly see that the temperature is between 21.6 °C and 21.7 °C. You might read it as 21.63 °C, but a second person could plausibly read it as 21.61 °C or 21.65 °C. With this scale you are sure of the first decimal place but uncertain of the second.
When quoting the result of a measurement, you should never quote more digits than you can justify in terms of the uncertainty in the measurement. The number of significant figures in the value of a measured quantity is defined as the number of digits known with certainty plus one uncertain digit. With thermometer A you could be sure of the 21 (two digits), but were uncertain about the digit in the first decimal place, so you can quote a reading to three significant figures, as 21.7 °C. With thermometer B it was the fourth digit that was uncertain, so you can quote your reading to four significant figures, as, for example, 21.64 °C.
Get some practice with identifying the number of significant figures in a number in this activity.
Activity 5 How many significant figures?
How many significant figures are quoted in each of the following quantities: 1221 m; 223.4 km; 1.487 km?
Answer
Each of the quantities is quoted to four significant figures.
If you measured the length of something as 13 mm, you would want to maintain the precision of your result if it was converted to centimetres or metres. Whether you write 13 mm or 1.3 cm or 0.013 m you are expressing the measurement to two significant figures. Why is 0.013 m only two significant figures rather than four though? You know that the uncertainty in your result hasn’t changed, so this shows that leading zeroes in decimal numbers do not count as significant figures.
Another circumstance in which you have to be careful about not using unjustified precision occurs when the results of measurements are used as the basis for calculations.
Suppose you had measured the diameter of a circular pattern to two significant figures as 3.3 cm. To calculate the radius you would divide this by 2 and get 1.65 cm. But is that how you should state the radius, as 1.65 cm is shown to three significant figures? That implies that the radius is more precise than the measurement made of the diameter. This clearly does not make sense, so the radius can only be shown to the same number of significant figures as the diameter. This means rounding it up to 1.7 cm, since the 3rd significant figure is 5 or more. If the 3rd significant figure had been 4 or less, then the value would have been rounded down.
Similarly, in any calculation you should make sure that your answer is no more precise than the least precise data that you started with. If you calculated the area of a rectangular pond with sides measuring 2.34 m and 4.2 m, the area should only be shown to 2 significant figures since there are only two significant figures in the least-precisely known value used in the calculation, the 4.2 m.
You also need to take care with large numbers with trailing zeros, such as 50 000. It is not clear whether this an exact number, or has been rounded to five, four, three, two or one significant figures. This ambiguity can be cleared up by using scientific notation. For example, if a length is measured to just one significant figure as 8 m, how should the equivalent value in centimetres be expressed? It would be misleading to write 800 cm, since that could imply the value is known to three significant figures. However if you use scientific notation 800 cm can be written as 8 × 102 cm making it clear that the quantity is known only to one significant figure, in line with the precision of the original measurement.
Worked example 4
The average diameter of Mars is 6762 km. What is this distance in metres, expressed to three significant figures?
Answer
The only way to express this quantity unambiguously to fewer than the four significant figures originally given is to use scientific notation.
The final digit is a 2, so no rounding up is required and the average diameter of Mars is 6.76 × 106 m to three significant figures.
Activity 6 More practice with significant figures
1. If the speed of light through glass is quoted as 2.0 × 108 metres per second, how many significant figures are being given?
Answer
Final zeroes are significant, so the speed is being given to two significant figures.
2. Neon gas makes up 0.0018% by volume of the air around us. How many significant figures are being given in this percentage?
Answer
Leading zeroes are not significant, so this value is also being given to two significant figures.
3. Express the following temperatures to two significant figures:
- a.−38.87 °C
- b.−195.8 °C
- c.1083.4 °C
Answer
a.The third digit is an 8, so the second digit must be rounded up:
–38.87 °C = –39 °C to two significant figures
b.There is no way of expressing a number greater than or equal to 100 unambiguously to two significant figures except by using scientific notation. The third digit is a 5, so again the second digit must be rounded up but as this is a 9 and rounds to 10, the 1st digit must be rounded up to 2.
{Note that the final zero in the intermediate rounded answer of -200 ° C is not included in the answer, as this would mean it was shown to 3 significant figures.}
c.Again, this quantity cannot be expressed unambiguously to two significant figures without using scientific notation. The third digit is an 8, so the second digit must be rounded up.
In your future studies of science and technology, you will be doing lots of calculations with numbers in scientific notation, and will also be expected to quote your results to appropriate numbers of significant figures.
Before completing this week you’ll now have the chance to practice the topics in the end-of-week quiz.