2.1 Right angled triangles – one known side, and two known angles
Take a look at the following Worked example and Activity.
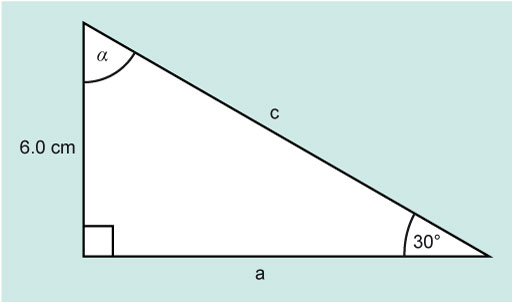
Worked example 1
In the example in Figure 6 there are three unknown values, α, a and c, and three known values.
The angle β is 30° and the side b is 6.0 cm. The right-angle is 90°.
The unknown angle α can be found using the fact that the sum of the internal angles of a triangle is 180°.
Now calculate a, which is ‘adjacent’ to the angle β, which is 30°. The opposite side is 6.0 cm.
If you look at SOHCAHTOA, you will find that the function relating adjacent and opposite is tan.
The side a is 10.39 cm.
The value for a has shown to 4 significant figures, rather than rounded to 2 significant figures at this point, to avoid introducing rounding errors in the final answer.
The only remaining unknown is c and this can be found using Pythagoras Theorem.
The side c is 12 cm. Using the rules for a triangle, some basic trigonometry and Pythagoras, and knowing the length of one side and the size of one angle, the remaining angles and sides of the triangle have been found.
Now try this one yourself.
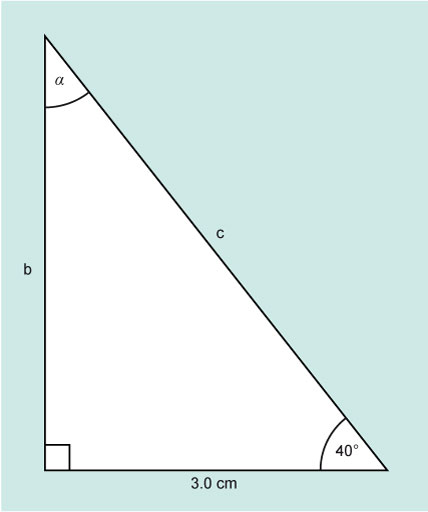
Activity 3 Find the unknown side
Find the unknown side b and c and the angle α for Figure 7.
Answer
You can start by finding angle α.
Since the right angle is 90°:
α + β = 90°
α = 90° – β
α = 90° – 40°
α = 50°
Now you can either find b or c.
Starting with c this time, which is the hypotenuse.
The function that links the adjacent (the known value) with the hypotenuse is cosine.
Rerranging to make c the subject:
c × cos 40° = 3.0 cm
So,
c = 3.916 cm
The opposite side b can be found using Pythagoras.
The length of side b is 2.5 cm (to 2 significant figures) and c 3.9 cm (to 2 significant figures).
Rounding both to two significant figures matches the precision with which the known side was shown.
The next section will consider the situation where angles α and β are unknown, but the length of two sides are known.