2.2 Right-angled triangles – two known values, and one unknown value
Take a look at the following Worked example and Activity.
Worked example 2
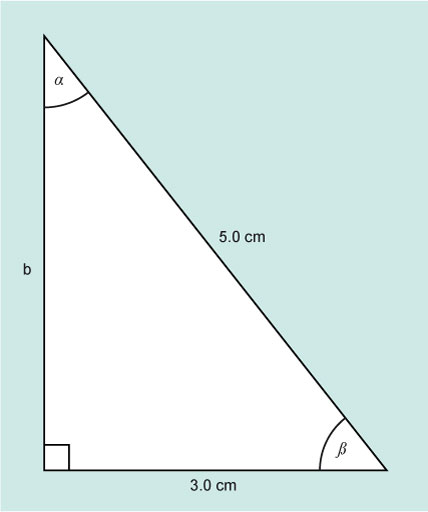
Figure 8 shows a right-angled triangle where the length of two sides are known, and just one angle – the right angle.
The aim is to calculate the values of α, β and b.
This time the length of two sides are known. In relation to the angle β, they are the adjacent and the hypotenuse.
the hypotenuse.The trig function which relates these two sides is cosine.
This means that β is the angle for which cos is 0.6; this can be written as β = cos–1 (0.6).
Cos–1 is the opposite, or inverse, of taking the cosine of an angle and will give the angle (between 0 and 180°) with the cosine value of 0.6. Fortunately, your calculator also does this for you.
Look at your calculator again. You should see a key which has the word shift or the letters inv above it. This key enables you to use the inverse functions on a calculator. Look at your sin, cos and tan keys again. Above each you should see what are known as the inverse functions, sin–1, cos–1 and tan–1.
Again depending on the calculator, you have you will either need to key in the function first, or the number. Either way cos–1 (0.6) = 53.13010236. So, β = 53° (to 2 significant figures)
α can now be found as before:
α + β = 90°
α = 90° – β
α = 90° – 53.13010236°
α = 37° (to 2 significant figures)
The opposite side b can be found using Pythagoras.
So, the length of side b is 4.0 cm.
Now have a go yourself in this next activity.
Activity 4 Find the angles
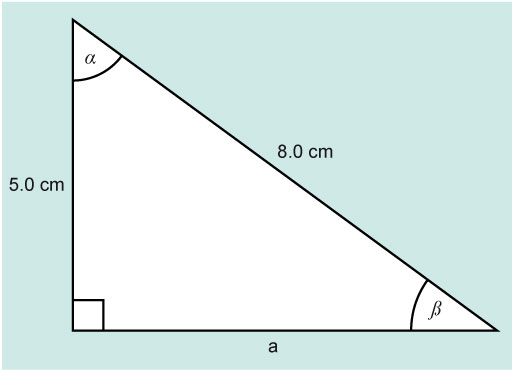
In the Figure 9, find the angles β and α and the length of side a.
Discussion
The known sides are the opposite and hypotenuse. The trig function that links these is sine.
and, since all the angles inside a triangle must add to 180°
α = 180° – (90° + 38.68°)
α = 51.32° (to 2 decimal places)
Now rounding to two significant figures to match the data in the question.
α = 51°
β = 39°
From Pythagoras:
The length of side a is 6.2 cm (to 2 significant figures).
So you know all the sides and all the angles in the triangle now.
Practicing new ideas and skills you have learned in maths is important, so here is one more activity for you to complete.
Activity 5 Finding sides and angle
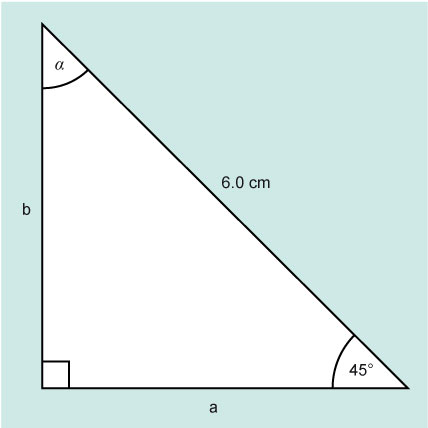
Look at Figure 10 and find the sides a and b and the angle α.
Discussion
The known sides are the opposite and hypotenuse. The trig function that links these is sine., but you still need to look for two known values related to one of the unknown values.
If you start by finding a (the adjacent), you need to use cosine as the adjacent and hypotenuse are related by that function.
You can now either use Pythagoras to work out b or the sine function.
You can check this using Pythagoras.
This gives the same value as using sine as expected.
To find the other angle:
This is a particular type of triangle where side a = side b and there are two equal angles.
This special sort of triangle is known as an isosceles triangle but is still also a right-angled triangle.
Trigonometry is powerful mathematical tool and the next section, before the weekly quiz, provides an example of trigonometry in practice.