Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Mathematics for science and technology
Mathematics for science and technology

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

3 Trigonometry in practice

One application of trigonometry that you might come across in applied mathematics, physics or technology courses concerns the resolution of forces. This enables a force acting in a certain direction to be shown as two component forces, at right-angles to each other.

Worked example 3

Timing: Allow about 15 minutes

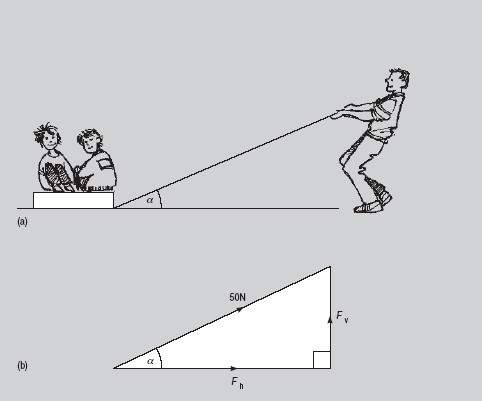
Consider the case of a father pulling his two young children along on a sledge (Figure 10a). He has a rope attached to the sledge which makes an angle α with the ground. Knowing that the force F on the rope is 50 N (newtons) and α is 25°, you can find the horizontal and vertical components of the force.

The force F acting in the rope may be considered as two component forces. The horizontal component can be called Fh and the vertical component Fv , as shown in Figure 11.

Using trigonometry to resolve forces.
Figure 11 Using trigonometry to resolve forces
Show description|Hide description

Using trigonometry to resolve forces. An illustartion which shows a man pulling two children who are sitting on a sledge. The sledge is being pulled using a rope or cable. The bottom section of the illustration shows a triangle.

Figure 11 Using trigonometry to resolve forces

Looking at Figure 11 and applying the trigonometry from earlier in this section, the following can be stated:

Fh is the adjacent, Fv is the opposite and 50 N is shown on the hypotenuse.

multiline equation row 1 cosine of alpha equals cap f sub h divided by 50 cap n

and

multiline equation row 1 sine of alpha equals cap f sub v divided by 50 cap n

Rearranging these two equations gives

multiline equation row 1 cap f sub h equals 50 postfix times cap n cosine 25 degree row 2 So comma cap f sub h equals 50 cap n prefix multiplication of 0.9063 row 3 cap f sub h equals 45.32 cap n row 4 cap f sub h equals 45 cap n left parenthesis to two significant figures right parenthesis

The horizontal component of the force is 45.32 N.

multiline equation row 1 cap f sub v equals 50 cap n sine 25 degree row 2 cap f sub v equals 50 multiplication 0.42262 row 3 equals 21.13 cap n row 4 equals 21 cap n left parenthesis to two significant figures right parenthesis

The vertical component of the force is 21 N.

Checking this using Pythagoras should show that Fh2 + Fv2 = F2

multiline equation line 1 45.32 squared postfix times equation left hand side prefix plus of 21.13 squared equals right hand side 2053.484 postfix times plus 446.515 line 2 equals 2500 line 3 equation left hand side equals right hand side 50 squared

This check gives extra confidence that the answer is correct.

Now here is an activity for you.

Activity 6 Calculating horizontal and vertical components

Timing: Allow about 10 minutes

Calculate the horizontal and vertical components of the force F in worked example 3 if:

  1. the angle α is reduced to 15°
  2. the angle α is increased to 45°.

Answer

  1.  
    multiline equation row 1 cap f sub h equals 50 cap n cosine 15 degree row 2 equals 50 cap n prefix multiplication of 0.9659 cap n row 3 equals 48.30 cap n row 4 equals 48 cap n left parenthesis to two significant figures right parenthesis

    The horizontal component of the force is 48 N.

    multiline equation row 1 cap f sub v equals 50 cap n sine 15 degree row 2 equals 50 cap n prefix multiplication of 0.2588 row 3 equals 12.94 cap n row 4 equals 13 cap n left parenthesis to two significant figures right parenthesis

    The vertical component of the force is 13 N.

  2.  
    multiline equation row 1 cap f sub h equals 50 cap n cosine 45 degree row 2 equals 50 cap n prefix multiplication of 0.7071 row 3 equals 35.36 cap n row 4 equals 35 cap n left parenthesis to two significant figures right parenthesis

    The horizontal component of the force is 35 N.

    multiline equation row 1 cap f sub v equals 50 cap n cosine 45 degree row 2 equals 50 cap n prefix multiplication of 0.7071 row 3 equals 35.36 cap n row 4 equals 35 cap n left parenthesis to two significant figures right parenthesis

    The vertical component of the force is 35 N.

You can check these values using Pythagoras.

  • a.48.302 + 12.942 = 502

  • b.35.362 + 35.362 = 502

Now look at the values you calculated in Activity 6.

Can you identify any relationship between the angle and the components of the forces?

As the angle α increases, the horizontal component of the force decreases and the vertical component increases. So, in order to maximise the effectiveness of the force in terms of horizontal motion, the angle α should be kept as small as possible.

The activities in this section have been designed to help you to use trigonometry in problem solving. As you continue your studies you will encounter other different applications.

Before completing this week you’ll now have the chance to practice the topics in the end-of-week quiz.