Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Mathematics for science and technology
Mathematics for science and technology

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

2.3 Brackets in mathematics

As you have seen, brackets are used to indicate, and clarify, the order in which a numerical calculation should be carried out. This is also true when you are using symbols, as in algebra.

So, for example considering 2(2n + 5) you should first multiple out the brackets. This means that all of the expression inside the brackets is multiplied by the figure outside them – a crucial idea to remember.

Thus multiline equation row 1 two times open two times n plus five close equals two multiplication two times n plus two multiplication five row 2 equals four times n plus 10

(Note, as a convention, 2(2n + 5) is preferable to (2n + 5)2, although, since it doesn’t matter what order you multiply two numbers in, they are equivalent.)

Here’s another example:

multiline equation row 1 a minus two times open a minus three close equals a minus two multiplication a minus two multiplication negative three row 2 equals a minus two times a plus six row 3 equals negative a plus six

The important point to note in this example is that everything in the bracket was multiplied by –2, not just 2.

Things become more complicated when you need to multiply two expressions both within brackets. For this you have to multiply each term, in both brackets by each other.

Let’s consider this example:

(a + 2)(b – 1)

It is easier to see the individual steps required by drawing lines between the terms in the expressions.

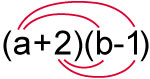
equation left hand side a multiplication b plus a multiplication negative one plus two multiplication b plus two multiplication negative one equals right hand side a times b minus a plus two times b minus two

If a = b

Then the expression becomes:

a2 + a – 2

Now have a go yourself in this activity.

Activity 2 Removing brackets

Timing: Allow about 10 minutes

Expand each of the following expressions by removing the brackets. Then (if possible) collect like terms.

  1. 2(2x – y)
  2. –2(a + 2b – c)
  3. 4(r + 6s) – (4s – r)
  4. x(2x – 3) – 2x(5 – 2x)
  5. (x – 2)(x + 3)
  6. (r + t)2
  7. (a – 4)(a + 4)
  8. one divided by three times open p minus six close squared

Answer

  1.       2(2x – y) = 4x – 2y
  2.       –2(a + 2b – c) = –2a – 4b + 2c
  3.  
    multiline equation row 1 four times open r plus six times s close minus open four times s minus r close equals four times r plus 24 times s minus four times s plus r row 2 equals five times r plus 20 times s
  4.  
    multiline equation row 1 x times open two times x minus three close minus two times x times open five minus two times x close equals two times x squared minus three times x minus 10 times x plus four times x squared row 2 equals six times x squared minus 13 times x
  5.  
    multiline equation row 1 open x minus two close times open x plus three close equals x squared minus two times x plus three times x minus six row 2 equals x squared plus x minus six
  6.  
    multiline equation row 1 open r plus t close squared equals open r plus t close times open r plus t close row 2 equals sum with, 4 , summands r squared plus r times t plus t times r plus t squared row 3 equals sum with, 3 , summands r squared plus t squared plus two times r times t
  7.  
    multiline equation row 1 open a minus four close times open a plus four close equals a squared minus four times a plus four times a minus 16 row 2 equals a squared minus 16
  8.  
    multiline equation row 1 one divided by three times open p minus six close squared equals one divided by three times open p minus six close times open p minus six close row 2 row 3 equals one divided by three times open p squared minus six times p minus six times p plus 36 close row 4 equals one divided by three times open p squared minus 12 times p plus 36 close row 5 equals one divided by three times p squared minus four times p plus 12

You should now feel more confident with simplifying algebraic expressions – don’t worry if some of these felt quite complex. The more practice you get the easier this will get.

Now it is time to look at how to rearrange equations.