3 Natural logarithms

The most frequently used bases for logarithms are 10 and the number ‘e’. Rather like , the irrational number ‘e’ occurs frequently in many branches of mathematics and its applications to science and engineering. Logarithms to base 10 are known as common logarithms and those to base ‘e’ are called natural or Napierian logarithms after the mathematician who discovered them.

Natural logarithms have the property that log_e e^x = x.

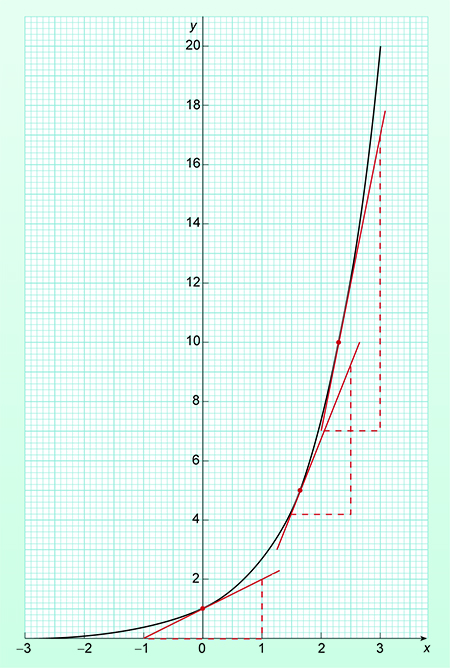
Natural logarithms are used to solve equations that contain the exponential function e^x where e is the irrational number 2.718281828 correct to ten significant figures. A graph of this function is shown in Figure 2.

Figure 2 The exponential function e^x

Show description|Hide description

The exponential function e^x shown in a graph.

Figure 2 The exponential function e^x

To work with natural logs on a calculator there is usually a button labelled log_e or ln, with the inverse e^x often accessed by the 2^nd function key.

The value of the constant e can easily be found by calculating the value of e¹.

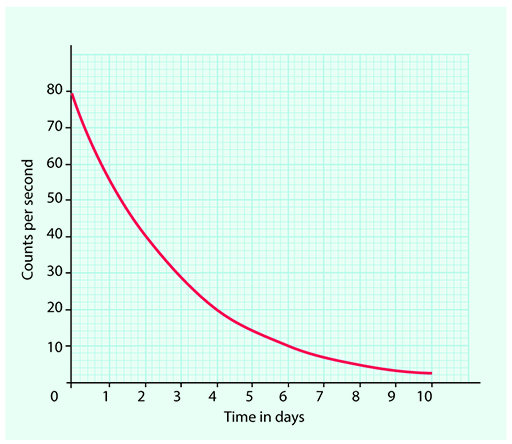
An example of an exponential function in science is radioactive decay. The half-life of a radioactive element is a constant value. This means that no matter how long the decay process has been continuing for it always takes the same time for the radioactivity to fall by half. If you compare Figure 2 to Figure 3 you should be able to see that they have similar shapes – although Figure 2 shows growth and Figure 3 decay.

Figure 3 Radioactive decay curve

Show description|Hide description

Radioactive decay curve shown in a graph.

Figure 3 Radioactive decay curve

When you work with logarithms to base 10 it is convention to drop the subscript and just write log x. Natural logarithms are written as In x. This means that the rules for logarithms, from section 2, can be written as follows for natural logarithms.

The final thing that you need to be able to do with logarithms is change the base.