2 Calculating probability

If a process is repeated in identical fashion a very large number of times, the probability of a given outcome is defined as the fraction of the results corresponding to that particular outcome.

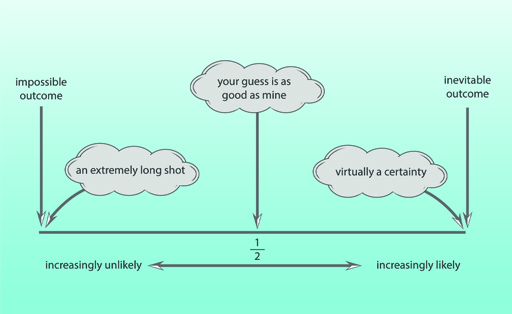
The nature of the fraction in Equation 1 shows that the probability of any given outcome cannot be smaller than 0 or larger than 1. A probability of 0 represents impossibility, while a probability of 1 represents inevitability. The closer the probability of a given outcome is to 1, the more likely that outcome is to occur. This is illustrated diagrammatically in Figure 1.

Figure 1 The scale of probabilities

Show description|Hide description

The scale of probabilities shown in a diagram. There are three main clouds, the first reads ‘an extremely long shot’ the second ‘your guess is as good as mine’ and a third ‘virtually a certainty’. The clouds are positioned on a scale which from left-to-right shows ‘impossible outcome’ to ‘inevitable outcome’.

Figure 1 The scale of probabilities

When a coin is tossed fairly, the likelihood of it landing on heads is equal to the likelihood of it landing on tails. If it is tossed repeatedly a great many times, it will in theory come up heads half the time: the probability of tossing heads is . The theoretical probability of tossing tails is, of course, also . The sum of these two probabilities ; i.e. it is certain that when the coin is tossed it will land either on heads or on tails. This is an example of a general rule:

The sum of the probabilities of all possible outcomes is equal to 1. A probability of 1 represents certainty.

Dice games involve rolling six-sided dice (singular ‘die’). Each face of a die is marked with a different score: one, two three, four, five or six. If the die is not loaded and the rolling is done fairly, then all outcomes are equally likely, so the probability of any one of the six possible outcomes (for example scoring a three) is . Again, the sum of the probabilities of all the possible outcomes is

So on one roll of the die the probability of scoring a three is and the probability of not scoring a three is . Another way of expressing this is to say that on a single roll of the die there is only one way of scoring a three, but there are 5 ways of not scoring a three. Clearly, it is more likely than not that a number other than three will be scored. This is just one illustration of another general rule:

The most likely outcome is the one that can occur in the greatest number of ways.

Provided nothing biases the result to make one outcome inherently more likely than others, the definition given by Equation 1 can be rewritten to encompass the number of ways in which a particular outcome may come about:

Use these ideas in this activity.

But what does a probability mean in real life?