5 Combining probabilities
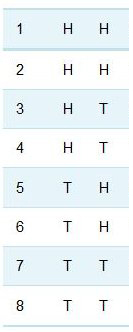
The probabilities described in Section 3 and Section 4 related to the outcomes of a single process, such as repeatedly tossing one coin. Now suppose you were to toss three separate coins simultaneously. What is the probability that they will show heads? One way of tackling this problem is to write all the possible combinations of results. There are in fact eight possible outcomes, all of which are equally likely, as the coins are assumed to be fair:
| 1 | H | H | H |
| 2 | H | H | T |
| 3 | H | T | H |
| 4 | H | T | T |
| 5 | T | H | H |
| 6 | T | H | T |
| 7 | T | T | H |
| 8 | T | T | T |
Figure 2 The possible comibination of results from tossing coins.
Of the eight combinations, only one – the top row – represents the desired outcome of three heads. On the basis of Equation 2, the probability of all three coins coming up heads is therefore .
The same result can be obtained using the ‘multiplication rule for probabilities’: the probability that the first coin will show heads is and the same is true for the second and third coins. The probability that all three will show heads is . It is important to note that in this situation the coins are tossed simultaneously, and how one coin lands is no influence on how another lands.
The multiplication rule is expressed in its most general form by saying that:
If a number of outcomes occur independently of one another, the probability of them all happening together is found by multiplying their individual probabilities.
An example of how this rule applies in a common genetic disease is given below.
Probability and cystic fibrosis
Cystic fibrosis is the most common genetic disease in white European and American populations. The cystic fibrosis (CF) gene is described as recessive, which means that individuals with only one copy of the gene, so-called ‘carriers’, show no symptoms of the disease and may be unaware that they carry the gene. Individuals with two copies of the faulty CF gene will show the symptoms of the condition.
Among white Europeans, the probability of being a carrier is .
For a child whose parents are both carriers, the probability of inheriting a copy of the CF gene from both parents is . This is therefore the probability that the child of such parents will have symptoms of the disease.
Do this next activity using this information on cystic fibrosis probabilities.
Activity 2 Probability and cystic fibrosis
Assuming that the CF gene is equally likely to be carried by men and women, what is the probability that any two white Europeans planning to have a child together would both be carriers?
Answer
The probability of both partners being carriers is
What is the probability of a child born to white European parents having cystic fibrosis?
Answer
The probability that both parents are carriers is , and the probability that a child whose parents are both carriers will have the disease is . So the probability of a child born to white European parents having cystic fibrosis is:
Activity 3 A pair of coins and dice
Calculate the combined probability in both these cases, remembering that the coins and dice cannot influence each other.
If you toss two coins at the same time, what is the probability of getting two tails?
If you throw a pair of dice, what is the probability of getting a pair of sixes?
Answer
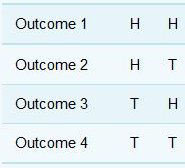
There are four possible outcomes, all of which are equally likely:
The outcome of two tails can occur in only one way, so the probability of getting two tails is .
This result can also be found from the multiplication rule:
the probability that the first coin will show tails is
the probability that the second coin will show tails is
so the probability of getting two tails is .
The probability of throwing a six with one die is . So the probability of getting a pair of sixes when throwing two dice is .
Another situation in which you might need to combine probabilities occurs when outcomes are mutually exclusive (i.e. cannot occur together). For example, what is the probability of getting either a three or a five on a single roll of a die? One way of working this out is to say that there are six possible outcomes altogether and two of them correspond to the desired outcome. So from Equation 2, the probability of the desired outcome is . The same result can be obtained using the ‘addition rule for probabilities’. The probability of throwing a three is and the probability of throwing a five is also , so the probability of throwing either a three or a five is . Again, this example illustrates a general rule:
If several possible outcomes are mutually exclusive, the probability of one or other of these outcomes occurring is found by adding their individual probabilities.
Worked example 1
One card is drawn from a shuffled pack of 52. What is the probability of the card being either a heart or a diamond? (For a description of a standard pack of cards, see the comment with Activity 1.)
Answer
The card cannot be both a heart and a diamond: these outcomes are mutually exclusive.
The probability of the card being a heart is .
The probability of the card being a diamond is .
So the probability of the card being either a heart or a diamond is:
(Note that since both diamonds and hearts are red suits, the question is equivalent to asking ‘what is the probability of a single card drawn from the pack being red?’ This was posed in Activity 1 and answered then by a different route, though of course the result was the same!)
Activity 4 The probability of mutually exclusive events
If you were to draw one playing card from a pack of 52, what would be the probability of that card being either the Jack, Queen or King of diamonds?
Answer
The probability of drawing any one particular card from the pack is . This is true for each of the three named cards. So the probability of drawing the Jack of diamonds or the Queen of diamonds or the King of diamonds is .
There are also cases in which both the addition and multiplication rules operate.
Worked example 2
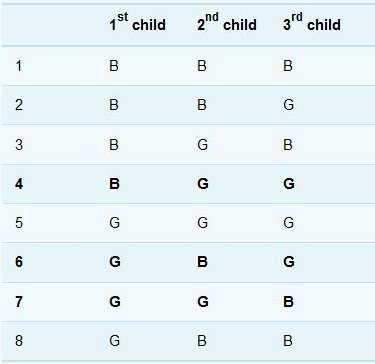
What is the chance that in a family of three children only one will be a boy?
Assuming that the sex of a child is independent of the sexes of its siblings, the probability that the first child is a boy is , the probability that the second is a girl is , and the probability that the third is also a girl is . So the probability of this particular combination (boy-girl-girl) is . But in a family with just one boy and two girls, the boy may be the eldest, the middle or the youngest child, and these possibilities are mutually exclusive. So the probability of the family consisting of a boy and two girls (born in any order) is
(Note that in fact the assumption that a baby is just as likely to be a boy as a girl is not quite true. UK statistics show that for every 100 girls born, 106 boys are born.)
As with the coin-tossing example earlier, you may find that a table of the possibilities helps in visualizing the situation. Of the eight possible combinations of three children, only three – shown in bold text – comprise one boy and two girls.
Activity 5 Another example using coins
If you toss two coins simultaneously, what is the probability of getting one head and one tail?
Answer
As in Activity 3, there are four possible outcomes, all of which are equally likely:
The outcome of a head and a tail can occur in two ways, so the probability of getting a head and a tail is .
This result can also be found from a combination of the multiplication and addition rules. For the combination of one head and one tail:
the probability that the coin on the left will be tails is ;
the probability that the coin on the right will be heads is ;
So the probability that the combination T H will occur is .
By similar reasoning, the probability that the combination H T will occur is also . These possibilities are mutually exclusive, so the probability of getting one head and one tails is .
Often with probabilities it is understanding how the events are linked, or not, that is the key to success. So, try and bear that in mind as you have a go at the quiz now.