Changing shapes

Learners will come up with several different ways of looking at the way these ‘houses’ grow. As you saw in Week 4, having multiple solution methods can give rise to fruitful algebraic reasoning if there is time planned in the lesson for learners to compare their methods, correct errors and explain why they are the same.

One very common method of describing the changing shapes is to focus on the 3 horizontal rows of matches. Another method is to note that each house has the same beginning and the same end. The middle section grows each time by adding 3 matches (1 each to the roof, the floor and the middle). We will now follow this second method to show its details.

The method is described in pictures, and then words and symbols. This sequence can be used for any methods.

Pictures (see Figure 8)

Figure 8 Growing houses

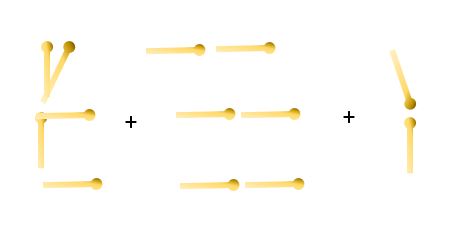
Words

The number of matches for the 10^th shape will be 5 (for the beginning) plus 2 (for the end) plus 3 for each of term added on after the first. You add one less group of 3 than the shape number.

Number symbols

It can be helpful for learners to see the calculations written as a sequence.

Shape 1: 5 + 2 or 7

Shape 2: 5 + 3 + 2 or 7 + 3

Shape 3: 5 + 3 + 3 + 2 or 7 + 3 + 3

Shape 4: 5 + 3 + 3 + 3 + 2 or 7 + 3 + 3 + 3

Now that we have got past 3 × 3, it is worth moving to multiplication instead of repeated addition.

Shape 5: 5 + 4 × 3 + 2 or 7 + 4 x 3

Words and algebraic symbols

Looking at the calculations shows a pattern. A method for finding the nth term is (starting with the part that changes) to calculate the number that is one less than n, multiply that by 3 and add it to 7.

In symbols this is (n-1) × 3 + 7. We can simplify this by expanding the brackets:

3n – 3 + 7

3n + 4.

So, the nth term of the sequence is 3n + 4.