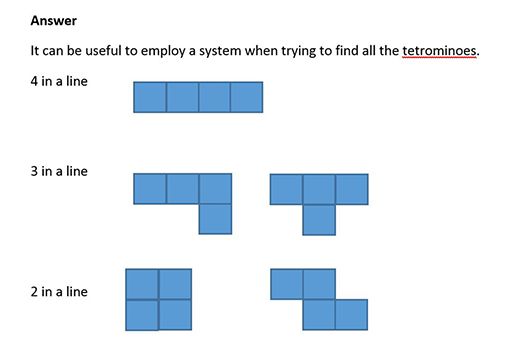
3.1 Polyominoes
The activities in this section can also be used to consider reflection and rotation symmetry.
You have probably seen dominoes, which are made of two squares joined together along their complete edges (Figure 10). There is only one domino because turning it round into a different orientation does not count as making another domino. A domino has two lines of symmetry (horizontal and vertical) and rotational symmetry of order 2 (2 positions where the domino can fit within a 360⁰ turn).
As you might imagine, triominoes are made of three squares placed along their complete edges. ‘Tri’ at the beginning of a word denotes three (like ‘triangle’ for a three-sided shape and ‘tricycle’ for a three-wheeler cycle).
There are two different triominoes (Figure 11). Remember that turning a triomino round or flipping it over does not create a different triomino.
Activity 11 The symmetry of triominoes
Describe the symmetry of each of the two triominoes.
- Does each triomino have reflection symmetry and, if so, where is the line of reflection?
- Does each triomino have rotation symmetry?
Discussion
The I-shape triomino has two lines of symmetry and rotation symmetry of order 2.
The L-shape triomino has one line of symmetry and rotation symmetry of order 1 (i.e. no rotation symmetry).
Activity 13 The pentominoes
Now try to find all 12 pentominoes (5 squares joined along their complete lengths).
Several challenges can be posed using the 12 pentominoes. It is useful to be able to give them labels, especially since many of them look like letters of the alphabet (with a little imagination). For example, one set of labels uses the letters F, I, L, N, P, T, U, V, W, X, Y and Z. See if you can match these letters to the pentominoes you made.
One challenge is to use all 12 pentominoes to make a 10 by 6 rectangle. 5 × 12, 4 × 15 and 3 × 20 rectangles are also possible. Other challenges are to make animals – a penguin, camel, dog and kangaroo are all possible.
Individual pentominoes can be used to make tessellations (or tiling patterns). For example, the P-shape and the F-shape can be tiled.