3 Fractions
What is a fraction?
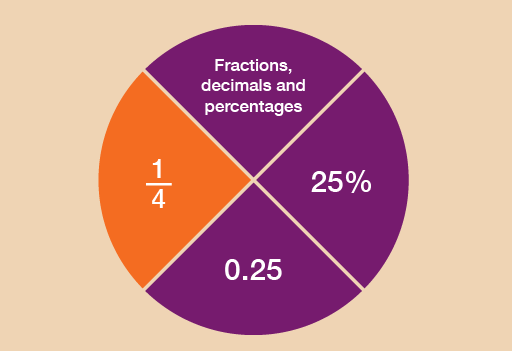
A fraction is defined as a part of a whole. So for example , or ‘one third’, is one part of three parts, all of equal size.
Fractions are an important feature of everyday life. They could ensure that you get the best deal when shopping – or that you receive the largest slice of pizza! As you go through this section, you’ll see how fractions could be used when you are shopping or within the workplace.
Fractions are related to decimals and percentages, which you’ll look at in the sections that follow this one.
This section will help you to:
- order and compare fractions
- identify equivalencies between fractions
- calculate parts of whole quantities and measurements (e.g. calculate discounts in sales).
Please look at the following example before you carry out the activity:
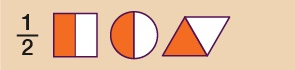
A half can be written as , i.e. one of two equal parts.
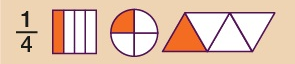
A quarter can be written as , i.e. one of four equal parts.
An eighth can be written as , i.e. one of eight equal parts.
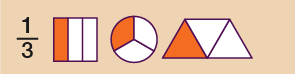
Hint: The top of the fraction is called the numerator. The bottom of the fraction is called the denominator. Any fraction with a 1 on the top is called a ‘unit fraction’, so , and , for example, are all unit fractions.
A fraction may not have a 1 on the top. For example, means ‘two out of three parts’, or ‘two thirds’.
Example: Where there’s a will, there’s a fraction
Lord Walton draws up a will to decide who will inherit the family estate. He proposes to leave of the estate to his son, to his daughter and to his brother.
- Who gets the biggest share?
- Who gets the smallest share?
Method
When numerators of fractions are all 1, the larger the denominator of the fraction, the smaller the fraction.
Looking at the example above, the fractions can be put in order of size starting from the smallest:
, ,
So:
- The biggest share () goes to his son.
- The smallest share () goes to his brother.
If you’re asked to arrange a group of fractions into size order, it’s sometimes helpful to change the denominators to the same number. This can be done by looking for the lowest common multiple – that is, the number that all of the denominators are multiples of.