5 Percentages
Like fractions and decimals, you’ll see plenty of references to percentages in your everyday life. For example:
This section will help you to:
- order and compare percentages
- work out percentages in different ways
- understand how percentages increase and decrease
- recognise common equivalencies between percentages, fractions and decimals.
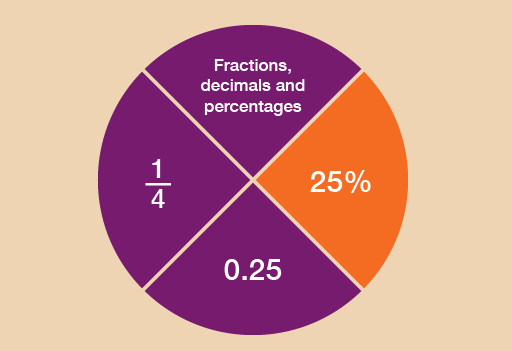
So what is a percentage?
- It’s a number out of 100.
- 40% means ‘40 out of every 100’.
- The symbol for percentage is %.
- 100% means 100 out of 100. You could also say this as the fraction .
You may have seen examples of percentages on clothes labels. ‘100% wool’ means that the garment is made entirely of wool and nothing else. ‘50% wool’ means that the garment is half made of wool, half made of other materials.
The following example shows how to work out a percentage of an amount.
Example: How can you calculate percentage reductions?
An online shop offers a 10% discount on a television that usually costs £400. How much discount do you get?
A percentage is a number out of 100, so 10% means ‘10 out of 100’. This could also be put as , or 10 hundredths.
There are different ways that percentages can be worked out. The method that you choose really depends on the numbers that you are working with.
Here are two methods for solving this problem:
Method 1
We start with finding 1%.
To find 1% of an amount, divide by 100 (which you practised earlier in this session):
400 ÷ 100 = 4
Once we know 1% of an amount, we can find any percentage by multiplying by the percentage we want to find. So to find 10%, we multiply the 1% figure by 10:
4 × 10 = 40
The discount is £40.
If you think of 10% as a large fraction, , you use the rule of dividing by the denominator (the bottom number in a fraction) and multiplying by the numerator (the top number).
There is an alternative method for finding the answer.
Method 2
A percentage is a number out of 100, so 10% is , which is the same as saying .
If we want to find out 10% of £400, that’s the same as finding out of £400:
400 ÷ 10 = 40
This gives us the answer £40.
If you can work out 10% of an amount, you can find lots of other percentages. Say, for example, you wanted to find 30% of £60.
First you find 10%, by dividing by 10 (method 2):
60 ÷ 10 = 6
30% is three lots of 10%, so once you know 10%, you multiply the amount by 3:
6 × 3 = 18
So 30% of £60 is £18.
Tips
- To find 20%, find 10% first and then multiply by 2.
- To find 5%, find 10% first and then halve the answer (divide by 2).
Which method do you prefer?
- Method 1 will work for any percentage and is a good method to use to find percentages using a calculator.
- Method 2 can be used to work out percentages in your head if the numbers are suitable.
There are some other quick ways of working out certain percentages:
50% = , so you can halve the amount (divide the amount by 2)
25% = , so you can divide the amount by 4 (or you can halve and halve again)
75% = , so you can divide the amount by 4 and then multiply by 3 (or you can find 50% and 25% of the amount, and then add the two figures together).
Use whichever method you prefer to help you with the following activities. Remember to check your answers once you have completed the questions.
Activity 34: Finding percentages of amounts
- You need to pay a 20% deposit on a holiday that costs £800. How much is the deposit?
Answer
Method 1
In order to identify how much the deposit is, you need to find out what 20% () of £800 is. To do this, first you need to find out 1% () of £800:
- 800 ÷ 100 = 8
So 20% () of £800 is:
- 8 × 20 = 160
The deposit is £160.
Method 2
In order to calculate 10%, or , you need to divide the number by 10:
- 800 ÷ 10 = 80
You now have 10% and you need 20%. Therefore you need to multiply your 10% by 2:
- 80 × 2 = 160
The deposit is £160.
- Work out the following using any preferred method without a calculator:
- a.50% of £170
- b.30% of £250
- c.25% of £120
- d.75% of £56
- e.80% of £95
- f.5% of £620
Answer
There are different ways you could have worked out the answers to these calculations. One method is suggested in brackets in each case, but you may have used a different method.
- a.£85 (170 ÷ 2 = 85)
- b.£75 (Finding 10% is 250 ÷ 10 = 25, so 30% = 3 × 25 = 75)
- c.£30 (120 ÷ 4 = 30)
- d.£42 (75% is ; 56 ÷ 4 = 14, and then 14 × 3 = 42)
- e.£76 (Finding 10% is 95 ÷ 10 = 9.50, so 80% = 8 × 9.50 = 76)
- f.£31 (Finding 10% is 620 ÷ 10 = 62, so 5% = 62 ÷ 2 = 31)