3.3 Average speed
You’ve probably seen one of these signs whilst travelling along the motorway through roadworks. Perhaps you were in an average speed check zone of 50 mph and found your speed had crept up to 55 mph – what do you do? Slow down! If you only slow down to the speed limit of 50 mph however, you may well find that you are still over the average speed limit! This is just one example of where average speed comes up in our daily lives.
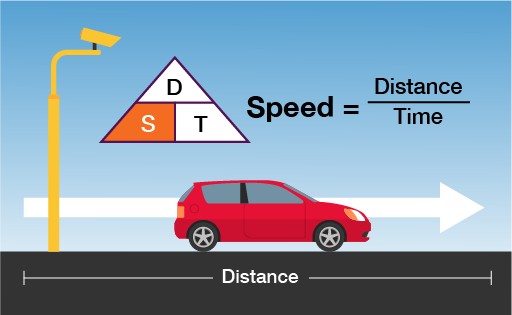
Being able to calculate and use average speed can help you to work out how long a journey is likely to take or, in the case of the example above, how much you need to slow down by in order not to exceed the average speed limit! The method for working out average speed involves using a simple formula.
You can also use this formula to work out the distance travelled when given a time and the average speed, or the time taken for a journey when given the distance and average speed.
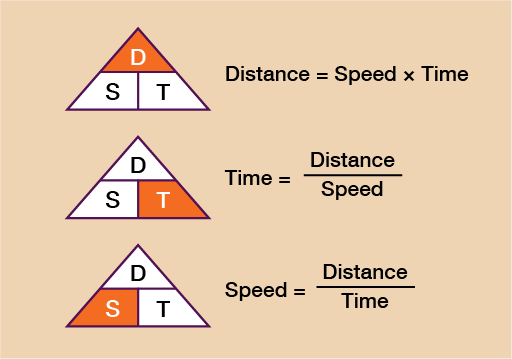
The formulas for this are shown in the diagram below.
You can see that when given any two of the elements from distance, speed and time, you will be able to work out the third. Let’s look at an example of each so that you can familiarise yourself with it.
Case study _unit3.3.4 Example: Calculating distance
A car has travelled at an average speed of 52 mph over a journey that lasts 2 and a half hours. What is the total distance travelled?
Method
You can see that to work out the distance you need to do speed × time. In this example then we need to do 52 × 2.5. It is very important to note here that 2 and a half hours must be written as 2.5 (since 0.5 is the decimal equivalent of a half).
You cannot write 2.30 (for 2 hours and 30 mins). If you struggle to work out the decimal part of the number, convert the time into minutes (2 and a half hours = 150 minutes) and then divide by 60 (150 ÷ 60 = 2.5).
Extract _unit3.3.1
52 × 2.5 = 130 miles travelled
Case study _unit3.3.5 Example: Calculating time
A train will travel a distance of 288 miles at an average speed of 64 mph. How long will it take to complete the journey?
Method
You can see from the formula that to calculate time you need to do distance ÷ speed so you do:
Extract _unit3.3.2
288 ÷ 64 = 4.5 hours
Again, note that this is not 4 hours 50 minutes but 4 and a half hours.
If you are unsure of how to convert the decimal part of your answer, simply multiply the answer by 60, this will turn it into minutes and you can then convert from there.
Case study _unit3.3.6 Example: Calculating speed
A Formula One car covers a distance of 305 km during a race. The time taken to finish the race is 1 hour and 15 minutes. What is the car’s average speed?
Method
The formula tells you that to calculate speed you must do distance ÷ time. Therefore, you do 305 ÷ 1.25 (since 15 minutes is a quarter of an hour and 0.25 is the decimal equivalent of a quarter):
Extract _unit3.3.3
305 ÷ 1.25 = 244 km/h
In a similar way to example 1, if you are unsure of how to work out the decimal part of the time simply write the time (in this case 1 hour and 15 minutes) in minutes, (1 hour 15 minutes = 75 minutes) and then divide by 60:
Extract _unit3.3.4
75 ÷ 60 = 1.25
Before moving on to the end-of-session quiz, have a go at the following activity to check that you feel confident with finding speed, distance and time.
Activity _unit3.3.3 Activity 7: Calculating speed, distance and time
Filip is driving a bus along a motorway. The speed limit is 70 mph. In 30 minutes, he travels a distance of 36 miles. Does his average speed exceed the speed limit?
A plane flies from Frankfurt to Hong Kong. The flight time was 10 hours and 45 minutes. The average speed was 185 km/h. What is the distance flown by the plane?
Malio needs to get to a meeting by 11:00 am. The time now is 9:45 am. The distance to the meeting is 50 miles and he will be travelling at an average speed of 37.5 mph. Will he be on time for the meeting?
Answer
You need to find the speed so you do: distance ÷ time.
The distance is 36 miles. The time is 30 minutes but you need the time in hours:
30 minutes ÷ 60 = 0.5 hours
Now you do:
36 ÷ 0.5 = 72 mph
Yes, Filip’s average speed did exceed the speed limit.
You need to find the distance so you do:
speed × time
10 hours 45 minutes = 10.75 hours
(If you are unsure, convert to minutes: 10 hours 45 minutes = 645 minutes, then divide by 60: 645 ÷ 60 = 10.75)
speed × time = 185 × 10.75 = 1988.75 km from Frankfurt to Hong Kong
You need to find the time so you do:
distance ÷ speed
50 ÷ 37.5 = 1.3
To covert this to minutes do:
1. × 60 = 80 minutes
80 minutes = 1 hour and 20 minutes
No, Malio will not make the meeting on time.
Box _unit3.3.1
Note: An answer of 1., means 1.3333333 (the 3 is recurring or never ending). It is conventional to write the digit that recurs with a dash above it.
Summary
In this section you have learned:
how to use timetables to plan a journey and how to calculate time efficiently
how to convert between units of time by using multiplication and division skills
how to use the formula for calculating distance, speed and time.