5 Negative numbers
Negative numbers come into play in two main areas of life: money and temperature. Watch the animations below for some examples.

Transcript
Negative numbers come into play in two main areas of life: money and temperature. If your bank balance is showing as -£250, this means that your balance is £250 below zero. In other words, you owe the bank £250.
Similarly, you'll be used to seeing winter weather forecasts predicting temperatures of -10 degrees Celsius. This means the temperature will be 10 degrees below zero degrees Celsius.
It can be useful to think of a thermometer if you're trying to find the difference between two numbers, where one or both of the numbers are negative. If the temperature is increasing, you go up the thermometer. If the temperature is decreasing, you travel down the thermometer.
For example, you'd like to know the answer to the sum [6 - 10]. Starting at number 6 on a thermometer and travelling down, it's easy to see that subtracting 10 will result in a number less than zero.
What is the answer to the sum [-5 + 12]? This time, we're starting below zero and travelling up the thermometer by 12 places, giving an answer of 7.
Can you work out the answer to the sum [-1 - 8]? In this example, we start below zero and the answer is also below zero: -9. Now try the next activity for more practise with negative numbers.
Activity 11: Negative and positive temperature
The table below shows the temperatures of cities around the world on a given day
| London | Oslo | New York | Kraków | Delhi |
|---|---|---|---|---|
| 4˚C | −12C | 7˚C | −3˚C | 19˚C |
a.Which city was the warmest?
b.Which city was the coldest?
c.What is the difference in temperature between the warmest and coldest cities?
Answer
a.Delhi was the warmest city as it has the highest positive temperature.
b.Oslo was the coldest city as it has the largest negative temperature.
c.The difference between the temperatures in these cities is 31˚C.
From 19˚C down to 0˚C is 19˚C and then you need to go down a further 12˚C to get to −12˚C.
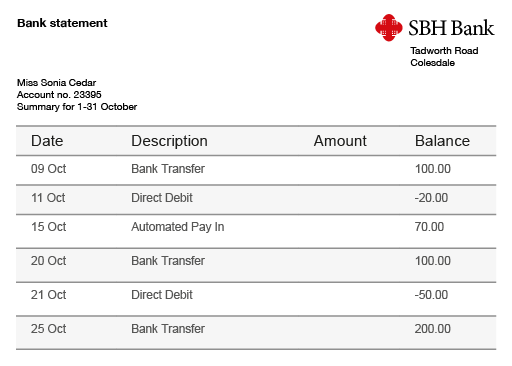
Look at this bank statement.
a.On which days was Sonia Cedar overdrawn, and by how much?
b.How much money was withdrawn between 9 and 11 of October?
c.How much was added to the account on 15 October?
Answer
a.The minus sign (−) indicates that the customer is overdrawn, i.e. owes money to the bank.
The amount shows how much they owe. So Sonia Cedar was overdrawn on 11 October by £20 and by £50 on 21 October.
b.£120 was withdrawn on 11 October.
The customer had £100 in the account and must have withdrawn another £20 (i.e. £100 + £20 = £120 in total) in order to be £20 overdrawn.
c.The customer owed £20 and is now £70 in credit, so £90 must have been added to the account.
Look at the table below showing a company’s profits over 6 months.
Hint: a negative profit means that the company made a loss.
| Month | Profit (£000) |
|---|---|
| January | 166 |
| February | 182 |
| March | −80 |
| April | 124 |
| May | 98 |
| June | −46 |
| Balance | Highlighted |
a.Which month had the greatest profit?
b.Which month has the greatest loss?
c.What was the overall balance for the six months?
Hint: start by calculating the total profits and the total losses.
Answer
a.February had the largest profit with £182 000 (remember to look at the column heading which shows that the figures are in 000s – thousands).
b.March showed the greatest loss at £80 000.
c.To calculate the overall balance you need to first calculate the total profits and the total losses. To calculate the profits you need to do this calculation:
166 + 182 + 124 + 98 = 570
So the profit was £570 000.
Next you need to calculate the total losses; two months showed a loss so you need to add these values:
80 + 46 = 126 so the losses over the six months were £126 000.
Now you can calculate the overall balance by subtracting the losses from the profits:
£570 000 − £126 000 = £444 000
This is a positive value so it means the company made an overall profit of £444 000.
Summary
In this section you have:
learned the two main contexts in which negative numbers arise in everyday life – money (or debt!) and temperature
practised working with negative numbers in these contexts.