1 Lewis Carroll, the master puzzler
Lewis Carroll (1832–1898), the British author of Alice in Wonderland and Alice through the Looking Glass, also published many logic puzzles. Here is one of them.
Suppose you are given the following starting points (called premises).
- All babies are illogical.
- Illogical persons are despised.
- Nobody is despised who can manage a crocodile.
What deduction can you make that uses all three of these premises?
One way to tackle this is by using Euler diagrams. The name comes from the Swiss mathematician Leonhard Euler (1707–1783), who had used them earlier than Venn.
The idea is that a set of things is represented by an oval. For example, this could be the set of babies. At this point you aren’t concerned with individual babies, just with babies as a class.
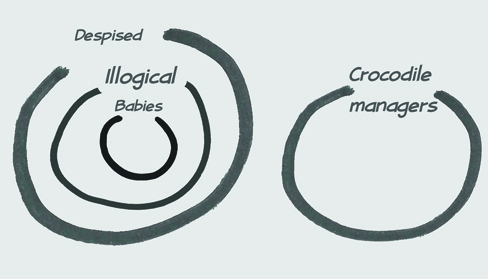
You can also consider the set of illogical persons. Premise 1, All babies are illogical, means the set of babies must be entirely contained in the set of illogical persons. You can represent the relationship like this.
From Premise 2, Illogical persons are despised, you can deduce that the set of illogical persons is entirely contained in the set of despised persons.
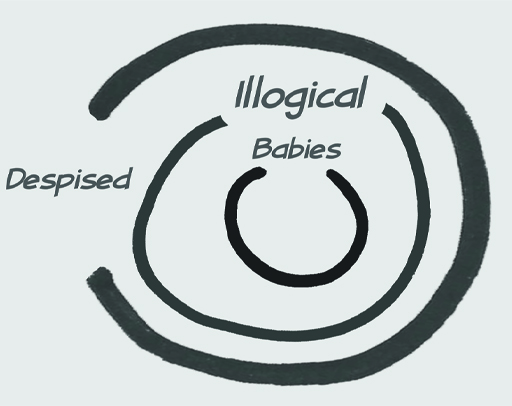
Finally, Premise 3, Nobody is despised who can manage a crocodile, implies that no crocodile managers are despised. This is represented in the Euler diagram by showing the set of crocodile managers as having no overlap with the set of despised people.
From this, you can see that the set of babies cannot have any overlap with the set of crocodile managers, and you reach the conclusion that
No babies can manage crocodiles.
You can try this using another logic puzzle in the following activity.
Activity 1 ‘No ducks waltz’
Consider the second Lewis Carroll logic puzzle below. What conclusion can you reach using all three of the premises given?
You could draw Euler diagrams, using pen and paper, but you may be able to solve the puzzle in some other way. If so, that’s fine. To solve it by Euler diagrams, you only need to use the two ideas you saw in the first example: sets enclosing one another and non-overlapping sets.
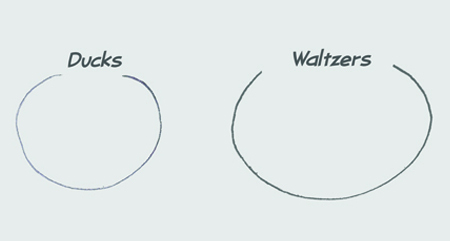
- No ducks waltz.
- No officers ever decline to waltz.
- All of Sue’s poultry are ducks.
Discussion
From Premise 1 you can draw this diagram.
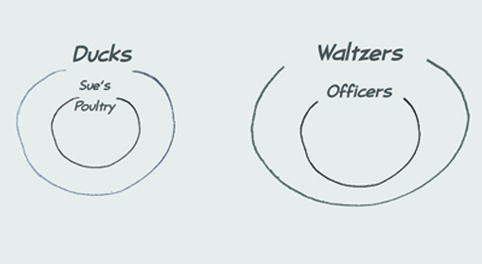
From Premise 2 you can see that all officers waltz.
Premise 3 says that Sue’s poultry are a subset of ducks
So, there is no overlap between Sue’s poultry and officers, and you reach the conclusion that none of Sue’s poultry are officers.
In the next section you will learn about some operations you can do with sets.