3 The size of a set
Every set has a size: how many members it contains. If a set has been stored in Python, you can find its size using len. For example, here is a set of numbers:
nums = {6, 3, 5, 1, 7, 9, 11, 4}
If you enter this into the Python shell below and then execute
>>> len(nums)
you should get 8.
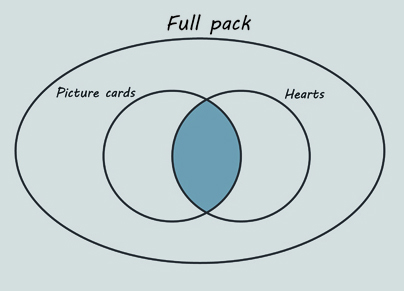
Euler diagrams are useful for reasoning about the size of sets. For example, consider the set of 52 playing cards in a standard pack (also called a deck). Figure 13 shows two smaller sets – picture cards and hearts – are contained in the overall set of size 52.
Picture cards are jacks, queens and kings, and there are 12 of these altogether, 3 per suit. There are 13 cards in each suit.
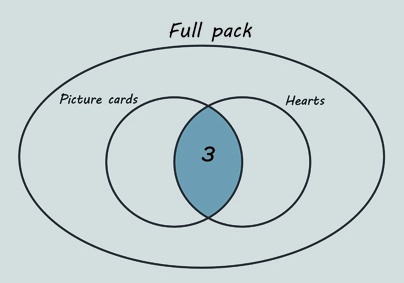
The shaded intersection in Figure 14 represents the picture cards that are also hearts. There are 3 of these.
You can continue to explore this in the next activity.
Activity 3 Figure it out
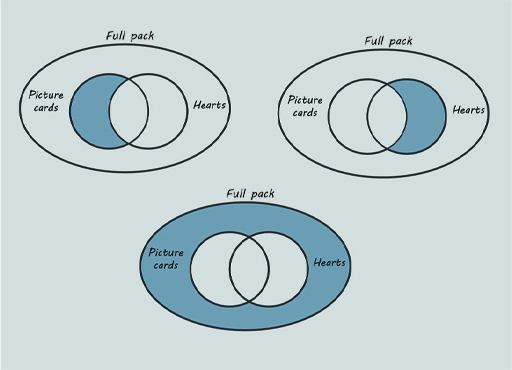
The shaded areas in the diagrams below represent, respectively:
- picture cards that are not hearts
- hearts that are not picture cards
- cards that are neither hearts nor picture cards.
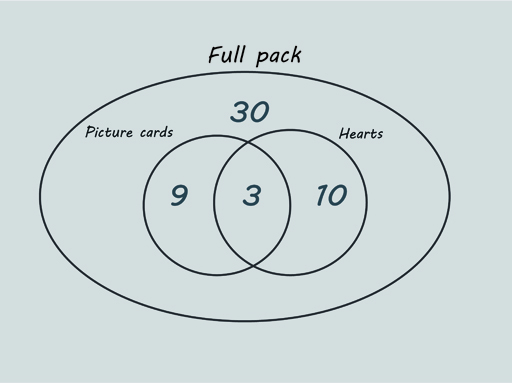
Using a pen and paper, copy the original Euler diagram and fill in the numbers for each of these regions.