2.3 The rise and fall of classical artificial intelligence
Artificial intelligence (AI) emerged as a field during the 1950s. In the USA, it was initially funded through programmes aimed at automatic machine translation. At the time of the Cold War (roughly from 1946 until 1991), the US government was concerned about tracking the communications of its adversary, the then Soviet Union. These communications were in Russian and there were so many of them that it was well beyond what could be done by human Russian-to-English translators. Automatic machine translation was viewed as a possible solution.
In this new field of AI, Leibniz’s dream was kept alive, despite the disappointing findings by mathematicians during the first half of the 20th century. The work of Doug Lenat (born 1950) illustrates how the field operated. Lenat initially made his name with a program that used rules of thumb to discover mathematical theorems. He believed that to arrive at a general artificial intelligence, most of human commonsense knowledge would have to be encoded. He began this enterprise – called the CYC project – in the 1980s. However, it ran into several obstacles.
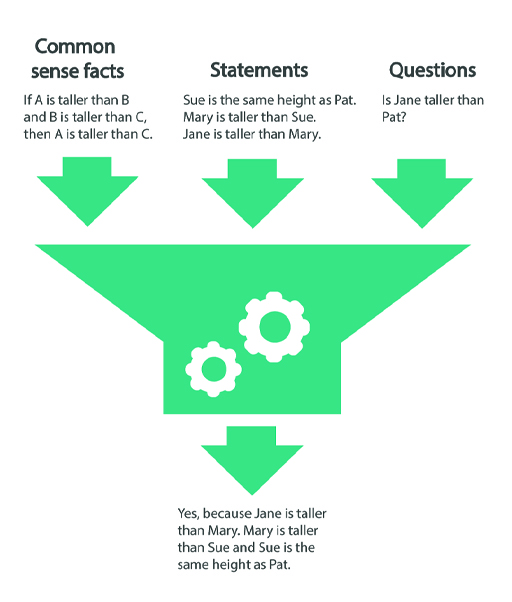
The idea was that the machine would be fed lots of commonsense facts and some further statements. If it was then asked a question, it would be able to compute an answer based on commonsense knowledge and the statements (see Figure 10).
You saw in Section 2.2 that even in mathematics, which deals with known axioms and relatively precisely stated proofs, it takes a large team many years to translate a human-authored proof into computer input. With commonsense knowledge, this problem is many times more challenging. This is because there are no neatly written-up lists of commonsense knowledge (unlike the axioms used by mathematicians). Of course, there are encyclopedias and other written sources, but much of our commonsense understanding of the world is rarely stated explicitly, if at all.
But forget that complication for a minute and suppose that commonsense knowledge can be translated into computer input. There are still the results of Gödel and Turing. Recall that they showed that there is no computer program that can tell whether a set of mathematical claims is true. Their results apply to claims in general (when stated with sufficient precision).
There is, however, a way out if we’re willing to put a limit on the kind of claims that can be dealt with. Let us entertain this possibility for the sake of the argument. To escape from Gödel’s and Turing’s results, we need to restrict our attention to claims that are precise but also sufficiently simple – that is, claims that are written in what is referred to as propositional logic (a notation system that is suitable for processing by a computer). A computer program can safely reason with such claims and determine whether they are true.
However, even if we limit the computer input to propositional logic, we are not out of trouble. In the 1970s, computer scientists working in the field of computational complexity theory discovered some new results. These results showed that reasoning with propositional logic is most likely to take an unfeasible amount of time as the size of the computer input grows. In this case, the input is the number of commonsense facts (in propositional logic) that are used in the reasoning. Since it is difficult to know in advance which commonsense facts are needed for a problem, this number is likely to be very large. That, in turn, means that it takes a very long time for a computer to answer any questions that require commonsense knowledge.
