1.1 Angles and lines
Angles measure the amount of turning from one position to another, so for example, you can describe how far around a circle you have moved. Imagine looking straight ahead and then turning around until you return to your starting position. The angle you have turned through is a full turn. If you turn so that you are facing in the opposite direction, you will have made half of a full turn. If you turn from looking straight ahead to facing either directly to your right or directly to your left, you will have made a quarter turn.
A full turn, or a circle, is defined as having 360º (said as 360 degrees). A circle is split into 360 equal parts, each part being 1º. Week 3 of Succeed with maths – Part 1 [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] looks at fractions by using pizzas, and this is very similar. This system was inherited from the Babylonians, whose counting system was based on 60 and who were the first people to use degrees in astronomy.
If one full turn is 360º, this means that a half turn is 180º and a quarter turn is 90º, as shown in Figure 1. This helps us to define some basic ideas in geometry.
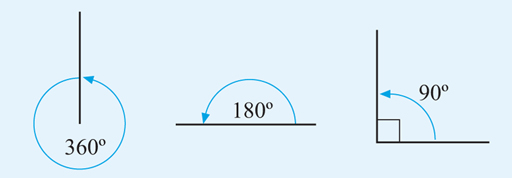
Figure 1 helps us to define some of the basic ideas of geometry.
These are:
- A circle is 360º.
- A straight line is 180º.
- A right angle is 90º.
Now, you’ve looked at one common way of measuring the amount of rotation, let’s think briefly about how to describe and show lines precisely.
Figure 1 shows a right angle, which is denoted by a small square drawn at the angle. This tells us that the angle is exactly 90º and not 89º or 91º. When two lines are at right angles to each other, they are also said to be perpendicular.
Lines that will never meet and are always the same distance apart, however far you extend them in either direction are called parallel lines. A railway track is an example of a set of two parallel lines and these are shown on diagrams by using an arrow (or double arrow) drawn on each line, as shown in Figure 2.
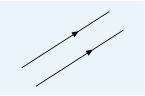
This use of precise language and definitions removes any confusion when you assess angles and lines on a diagram. These also allow us to move onto looking at shapes and the angles and lines that these are constructed from, in the next section.
