4 Length: imperial measurements
Before the 1970s, the UK used the imperial system of measurement, which had its basis in historical measurements and the need to have common weights and measures to enable the sale of goods and services to operate efficiently. For example, the foot, a measurement of length of around 30 cm (or the length of standard ruler), was first defined in law by Edward I in 1305, and is thought to be derived from the length of a man’s foot with shoes.
For those not brought up using the imperial system for measurement it may seem to be a very difficult way to measure things. It does not operate on a system of base units and standard prefixes, like the SI, so this means that there are lots of different relationships to remember for each set of measurements. These are also not based upon the number ten (as the SI is), so calculations and conversions between units isn’t quite so straightforward.
However, the same techniques can be used to help decide whether you need to divide or multiply when converting, as you’ll see.
The common units used for measuring length in the imperial system are inches (in), feet (ft), yards (yd) and miles (mi). These units are listed in increasing order of size.
If you haven’t worked in these units before you may not have a good idea of their actual sizes. Table 2 below shows approximate values for how the imperial units relate to the SI units to help with this.
| Imperial unit | SI unit |
|---|---|
| 1 inch | 2.5 cm |
| 1 foot (singular of feet) | 30 cm |
| 1 yard | 0.9 m |
| 1 mile | 1.6 km |
Now back to how these imperial units of length relate to each other.
There are:
- 12 inches in one foot
- 3 feet in one yard
- 1760 yards in one mile.
So as you can see, no regular relationship based on tens here!
This means that when you convert between the different units of length it becomes more important to think carefully about the answer that you will be expecting. Should it be bigger or smaller than the number you started with?
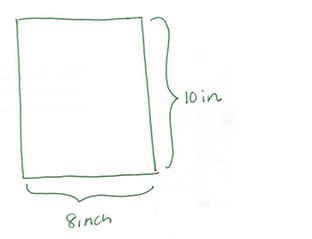
Let’s have a look at an example before you have a go yourself. If you have a photograph that measures eight inches by ten inches, as shown in Figure 2, what is the total distance around the photo in feet and inches?
The top and bottom of the photo have the same measurement, eight inches. Similarly, the left- and right-hand sides share a measurement of ten inches.
Or as there are two sides measuring 8 inches and two sides measuring 10 inches:
Now looking at how many feet there are in 36 inches:
You already know that:
So if a measurement is in feet instead of inches, the converted number should be smaller than the original. This means the number of inches has to be divided by 12. So,
This means that 36 inches is the same as 3 feet. Thus, the length of the border of the picture is 3 feet.
Now it’s your turn. Remember to think about the size of the final answer you are expecting.
Activity 2 Length in imperial units
For each of the following scenarios, use the appropriate operation, multiplication or division, and unit to determine the answer. Click on ‘reveal comment’ if you would like a hint to get going.
- a.The height of a three-year-old girl is measured as 34 inches. Over her lifetime, she grows another 34 inches. When fully grown, how tall is she in feet and inches?
Comment
If you have studied Succeed with Maths Part 1 you may remember that drawing pictures can help to visualise a situation.
Answer
a.The girl is 34 inches when she is three and then grows another 34 inches before reaching her full height.
There are two ways to calculate the final height, and either is perfectly fine!
Or
So for a measurement using feet instead of only inches, the number should be smaller than the original. This means the number of inches has to be divided by 12.
This is the same as 5 feet and 0.67 feet.
Now convert 0.67 feet into inches.
This time you are converting from a larger to a smaller unit, so you need to multiply.
This means 68 inches is the same as 5 feet and 8 inches.
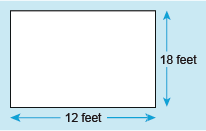
- b.A rectangular garden measures 12 feet by 18 feet. What is the length of the border of the garden in yards?
Answer
- b.Here’s a quick sketch of the garden to help visualise the problem:
Just as with the photo frame problem, to calculate the length of the border you need to first add the length of all the sides together.
As you are converting from a smaller to a larger unit, you would therefore expect the converted answer to be smaller than the original value. Hence, you need to divide in this case.
So the
Thus, the length of the garden’s border is 20 yards
Now you’ve looked at units of length in both the SI and the imperial system, it’s time to look at converting between the systems of measurement in the next section.