2 Sine, cosine and tangent
Sin, cos and tan are the commonly used abbreviations for each function. So:
- Sin = sine
- Cos = cosine
- Tan = tangent
Sine is pronounced as ‘sign’ and cosine as ‘co-sign’.
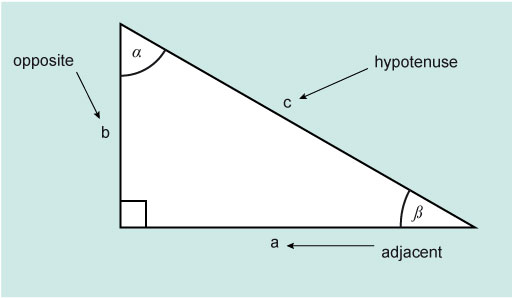
Based on the triangle in Figure 2 these functions are defined as follows:
There is an easy way to remember this: SOHCAHTOA (pronounced sock -ah- toe-a).
Using these functions, and Pythagoras theorem, if you know two sides or a side and an angle for a right-angled triangle, then you can find the other side, sides or angle as required.
Activity 2 Sine and cosine values between 0° and 90°
Making sure that your calculator is still set to degrees, work out these values for sine and cosine.
| 1. | Sin 0° |
| 2. | Cos 0° |
| 3. | Sin 10° |
| 4. | Cos 10° |
| 5. | Sin 25° |
| 6. | Cos 25° |
| 7. | Sin 45° |
| 8. | Cos 45° |
| 9. | Sin 70° |
| 10. | Cos 70° |
| 11. | Sin 90° |
| 12. | Cos 90° |
Do you notice anything interesting about your answers?
Answer
| Angle/degrees | Sine | Cosine |
|---|---|---|
| 0 | 0 | 1 |
| 10 | 0.1736 | 0.9848 |
| 25 | 0.4226 | 0.9063 |
| 45 | 0.7071 | 0.7071 |
| 70 | 0.9397 | 0.3420 |
| 90 | 1 | 0 |
Perhaps you noticed that all the values for sine and cosine seem to lie between 0 and 1 for angles between 0° and 90°.
You may have also observed that as the values for sine increase, the values for cosine decrease.
In fact, for any angle between 0° and 90° the values for sine and cosine lie between 0 and 1.
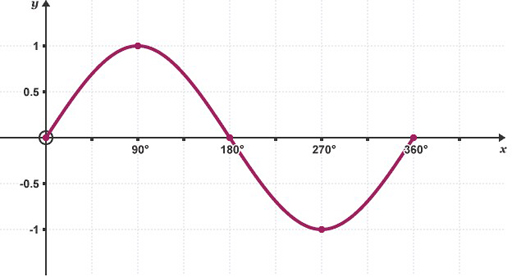
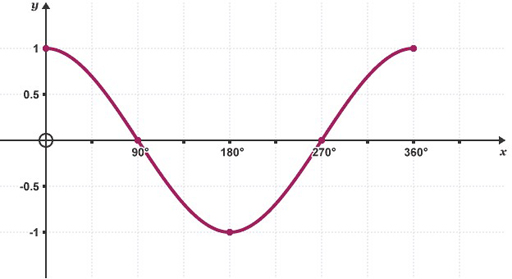
These two graphs (Figures 3 and 4) show the shape of the sine and cosine functions between 0 and 360°. From this you can see that both functions stay within –1 and +1.
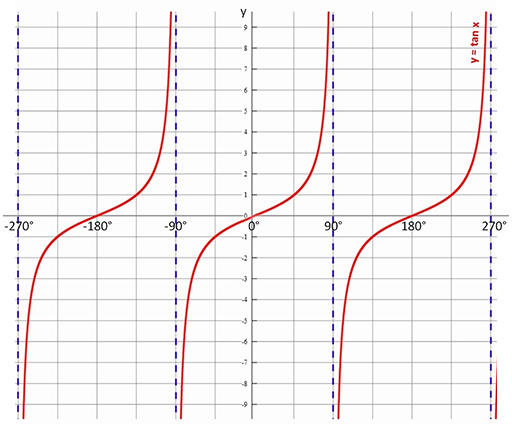
As shown in Figure 5 the tangent function is not similar in the way that cosine and sine are but forms its own repeating pattern.
Now it is time to see how you can use these functions with right-angled triangles.