1.1 Writing algebraic expressions
In this section you will write some algebraic expressions which arise from a simple problem.
Activity 1 Triangle perimeters
The shape in Figure 1 is made of two congruent triangles. Each triangle has sides labelled 3 cm, a cm and b cm. Find an expression, in terms of a and b, for the perimeter of the combined shape. You do not need to simplify it.
Find another expression. And then find another.
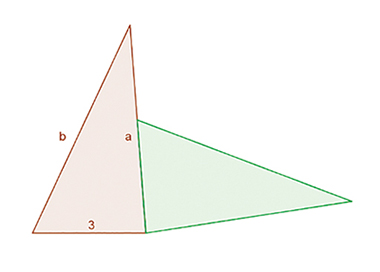
The purpose of this task is to work with unknown quantities – the side lengths a and b and the perimeter – which can be represented in different ways: as (labelled) parts of the diagram, in words and in symbolic expressions. A good way to start is by reminding yourself what perimeter means, and by labelling the side lengths of the green triangle (which one is 3 cm long and which is a cm?).
There are different methods for calculating a perimeter, and each of these could give rise to a different symbolic expression. This is the reason for asking you for ‘another expression. And then another’. People working on this task in a group are likely to find a range of symbolic expressions but if they simplify these, they should all come to the same result.
For many learners, handling the congruent triangles will help them perceive how the combined shape is made, which sides are the same length and how to express the ‘leftover bit’ as a difference or a subtraction. We have avoided using right-angled triangles (so as not to remind you of Pythagoras’s Theorem) but this is not a distraction for younger learners. They can cut a rectangle in half diagonally, label the shortest side 3 units, and rearrange the pieces.
Discussion
Teachers have found that a key feature of encouraging early algebraic thinking is productive lingering. This is a phrase to describe asking learners to compare and explain their answers when they are still in the form of expressions that show the thinking processes and the mathematical operations in a calculation, and before they are tidied into a final answer.
Learners can express their method in words, or as a calculation using numbers, or, eventually, as an algebraic expression. These word- or number-based expressions can be called mathematical sentences, and they are the foundations of algebraic thinking.
In Japanese classrooms, teachers have a special word for the expression that leads to a final answer. It is called the ‘shiki’. Teachers ask their learners to work out what is the appropriate shiki to use for a problem, and ask them to say the shiki as well as the final answer.
Activity 2 Reflecting
How many expressions did you find for the perimeter?
In the table below, match the algebraic expressions with the corresponding explanation in words.
| 1 | P = (a + b + 3) – 3 + (a + b + 3) – 3 | A | On the green triangle it’s only a and b because the 3 is missing. On that one it’s 3 and b and a but then you’ve got to take 3 away again. | |
| 2 | (a + b) + 3 + b+ a – 3 | B | The perimeter is 3 add side b then it’s the little bit down there, then it’s add side b and side a. That bit is what’s left over when you put the 3 next to a. | |
| 3 | P = 3 + b + (a – 3) + b + a | C | To make the perimeter – for each whole triangle it’s a plus b plus 3, but it’s missing 3 from each one. | |
| 4 | (a + b + 3) + b + (a – 3) | D | Count all the sides, it’s a plus b plus 3, doubled, and then you miss out 3 twice. | |
| 5 | 2 (a + b + 3) – 2 x 3 | E | That side is the same as the missing side so you have all of one triangle. For the other triangle you have side b and just a bit down side a, a less 3. |
Discussion
All of the expressions are equivalent to 2a + 2b but they represent different thinking processes.
You should have matched 1C, 2A, 3B, 4E, 5D.
The next section examines the idea that you can express mathematical reasoning in words or in algebraic expressions. The mathematical reasoning that you are doing in this task is giving instructions for calculations without actually doing the calculation.
