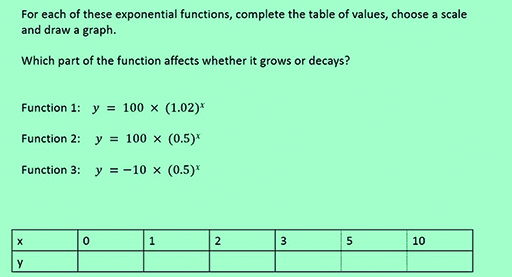
3.3 The exponential function
In the next two activities you will meet one last important type of function and graph: the exponential function.
Activity 9 Word of mouth
Three friends share a secret. On day 2 they each tell one new person.
Then every day for a week, everyone who knows the secret tells it to one new person.
How many people know on day 2?
How many people know on day 3?
Estimate how many people will know the ‘secret’ on day 8.
Discussion
On day 2, 6 people know the secret.
On day 3, 12 people know.
This is a sequence you met before: 3, 6, 12, 24, 48. The term-to-term rule is ‘double each term to get the next’. The position-to-term rule is 3 × 2n-1.
By day 8, a large number of people will know. You can use the formula or a graph to find the value (Figure 14).
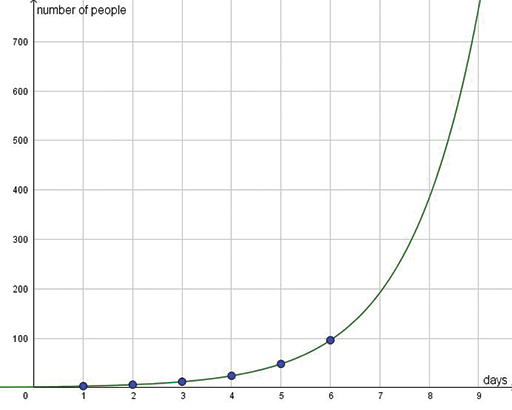
In this problem, the number of new people who learn the secret each day is equal to the number who know it already. This makes it an example of an exponential function. The characteristic feature of these functions is that their rate of change is proportional to their value. In more everyday words, this means that the higher the y-value, the more it grows.
It is worth comparing this with a linear function, which grows at a constant rate.
This feature lies behind the English phrase ‘growing exponentially’ which is used to emphasise rapid growth. It also makes exponential functions difficult to graph. The scale on the y-axis has to be large to include the points for higher values of x, but then the y-values for low values of x are not easy to read.
As well as exponential growth you can have exponential decay, which gives a decreasing exponential function.
Activity 10 Exploring exponentials
Exponential functions are used in many real-life situations.
- In biology, they describe the spread of diseases and the growth of populations.
- In engineering, they describe waves, and how movement dies away.
- In finance, they describe how money grows when it is invested at a constant rate of interest.
Although exponential functions appear on the school curriculum for the middle years, learners are expected to plot and read their graphs and not to work with their equations. This has been included only for your own knowledge asa teacher.
The role of teachers is to support learners in gaining a good mathematical understanding of graphical representation in a range of contexts. Learners need to be able to choose scales and plot x-values and y-values on a graph. They need to find the y-value for a given x-value and vice versa. They also need to interpret change on a graph. They need to know whether the graph is increasing or decreasing, and whether changes are constant or can vary. The linear, piece-wise linear, reciprocal and exponential graphs are all functions that illustrate different kinds of change and this is their value for teachers.