1.1 Converting units of measure in the same system
Imagine you are catering for a party and go to the wholesale shop to buy flour. You need 200 g of flour for each batch of cookies you will be making and need to make 30 batches. You can buy a 5 kg bag of flour but aren’t sure if that will be enough.
In order to work out if you have enough flour, you need both measurements to be in the same unit – kg or g – before you can do the calculation. For units of measure that are in the same system (so you are not dealing with converting cm and inches for example) it’s a simple process to convert one measurement into another.
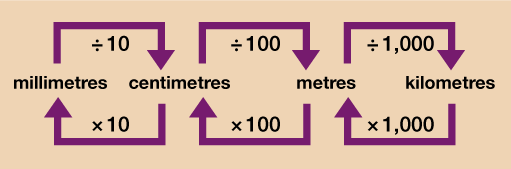
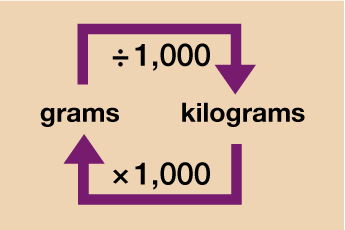
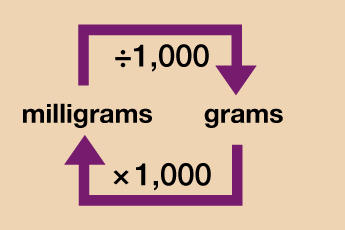
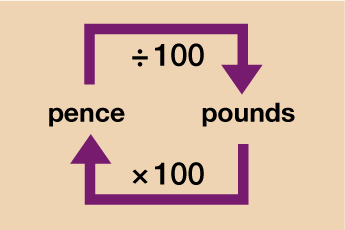
For now we will focus on what is known as the metric system of measurement (we will look at some units from the imperial system later on in the session). In most cases, if you want to convert between units in the metric system you will just need to multiply or divide by 10, 100 or 1000.
Take a look at the diagrams below which explain how to convert each type of measurement unit.
Length
Weight
Money
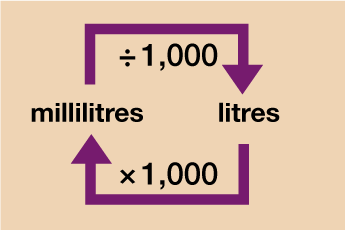
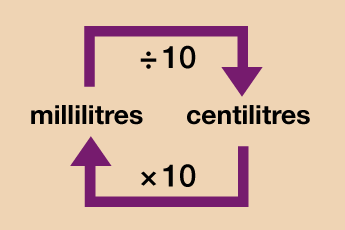
Capacity
Note: Capacity may also be measured in centilitres (shortened to cl). On a standard bottle of water, for instance, it may give the capacity as 500 ml or 50 cl – there are 10 millilitres (ml) in 1 centilitre (cl).
When converting between units you may need to do the conversion in stages.
Example: Converting length
You measure the gap for a washing machine to be 0.62 m. You look on a retailer’s website and it shows the width of a particular washing machine to be 600 mm. Will this fit in the gap?
Method
You can convert the gap for the washing machine in stages. Convert from metres to centimetres first by multiplying by 100:
0.62 m × 100 = 62 cm
Now convert the centimetres figure into millimetres by multiplying by 10:
62 cm × 10 = 620 mm
So the washing machine (600 mm wide) will fit in the gap of 620 mm.
You may have preferred to convert the washing machine width into metres instead and do the comparison that way:
600 mm ÷ 10 = 60 cm
60 cm ÷ 100 = 0.6 m
0.6 m is less than 0.62 m so the washing machine will fit the gap.
You’ll learn how to convert between different currencies and units of measure in different systems (metric system kilograms (kg) to imperial system pounds (lb) for example) later in this session. For now, have a go at the activities below and test your metric conversion skills.
Activity 2: Converting units
Use your conversion skills to fill in the missing information in Table 1(a). You may want to carry out some of the calculations in stages.
Please carry out all of your calculations without using a calculator. However, double-check on a calculator if you need to.
| Length | Weight | Capacity |
| 55cm = ? mm | 9.75 kg = ? g | 235 ml = ? l |
| 257 cm = ? m | 652 g = ? kg | 18.255 l = ? ml |
| 28.7 km = ? m | 5846 g = ? kg | 16 ml = ? l |
| 769 mm = ? cm | 19.4 kg = ? g | 7.88 l = ? ml |
| 1.43 m = ? mm | 44 g = ? mg | 250 ml = ? cl |
| 125 500 cm = ? km | 750 000 mg = ? kg | 7.4 l = ? cl |
Answer
| Length | Weight | Capacity |
| 55cm × 10 = 550 mm | 9.75 kg × 1000 = 9750 g | 235 ml ÷ 1000 = 0.235 l |
| 257 cm ÷ 100 = 2.57 m | 652 g ÷ 1000 = 0.652 kg | 18.255 l × 1000 = 18 225 ml |
| 28.7 km × 1000 = 28 700 m | 5846 g ÷ 1000 = 5.846 kg | 16 ml ÷ 1000 = 0.016 l |
| 769 mm ÷ 10 = 76.9 cm | 19.4 kg × 1000 = 19 400 g | 7.88 l × 1000 = 7880 ml |
| 1.43 m × 100 = 143 cm × 10 = 1430 mm | 44 g × 1000 = 44 000 mg | 250 ml ÷ 10 = 25 cl |
| 125 500 cm ÷ 100 = 1255 m ÷ 1000 = 1.255 km | 750 000 mg ÷ 1000 = 750 g ÷ 1000 = 0.75 kg | 7.4 l × 100 = 740 cl |
Activity 3: Solving conversion problems
Solve the following problems. Please carry out all of your calculations without using a calculator. You may double check on a calculator if needed.
- A sunflower is 1.8 m tall. Over the next month, it grows a further 34 cm. How tall is the sunflower at the end of the month?
- Peter is a long distance runner. In a training session he runs around the 400 m track 23 times. He wanted to run a distance of 10 km. How many more times does he need to run around the track to achieve this?
- A water cooler comes with water containers that hold 12 l of water. The cups provided for use hold 150 ml. A company estimates that each of its 20 employees will drink 2 cups of water a day. How many 12 l bottles will be needed for each working week (Monday to Friday)?
- David is a farmer and has 52 goats. He is given a bottle of wormer that contains 0.3 litres. The bottle comes with the instructions:
- ‘Use 4 ml of wormer for each 15 kg of body weight.’
Answer
- 1 m = 100 cm so 1.8 × 100 = 180 cm
180 cm + 34 cm = 214 cm or 2.14 m
- 400 m × 23 = 9200 m that Peter has run.
1 km = 1000 m so, 10 km = 10 × 1000 = 10 000 m
The difference between what Peter wants to run and what he has already run is:
- 10 000 − 9200 = 800 m
- 800 ÷ 400 = 2
Peter needs to run another 2 laps of the track.
- 1 litre = 1000 ml so 12 l = 12 × 1000 = 12 000 ml
Each employee will drink 2 × 150 ml = 300 ml a day
There are 20 employees so 300 × 20 = 6000 ml for all employees per day
A working week is 5 days:
- 6000 × 5 = 30 000 ml for all employees for the week
- 30 000 ÷ 12 000 = 2.5
They will need 2 and a half containers per week.
- 1 litre = 1000 ml so 0.3 litres = 0.3 × 1000 = 300 ml of wormer in the bottle
52 goats at 21 kg each is 52 × 21 = 1092 kg total weight of goats
To find the number of 4 ml doses required do:
- 1092 ÷ 15 = 72.8
- 72.8 × 4 ml = 291.2 ml of wormer needed.
Yes, David has enough wormer.
Hopefully you will now be feeling confident with converting units of measure within the same system. You’ll need to know how to do this and be able to remember how to convert from one to another by multiplying or dividing. If you need further practice converting between units, please revisit the ‘Units of measure’ session in the Everyday Maths 1 course.
If you are being asked to convert between units in different systems (e.g. between litres and gallons) or between currency (e.g. US dollars and British pounds), you won’t be expected to know the conversion rate – you’ll be given it in the question. The next section will show you how to use these conversion rates and you’ll be able to practise solving problems that require you to do this.
Summary
In this section you have learned:
- that different units are used for measurement
- unit selection depends on the item or object being measured
- how to convert between units in the same system.