5.2 Scales and measuring instruments
Now you’ve worked through some examples have a go at the following activities.
Activity 10: Reading scales
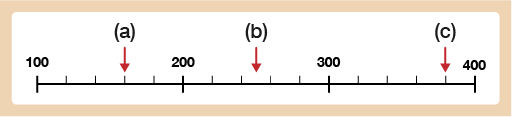
Read the scales below and find the values the arrows are pointing to for (a), (b) and (c).
Answer
The scale is going up in steps of 20 (the numbered markers are going up in intervals of 100 and there are 5 small steps between each numbered marker: 100 ÷ 5 = 20) so the answers are:
a.160
b.This is halfway between 240 and 260 so the answer is 250
c.380
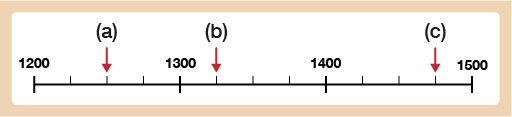
Read the values for (a), (b) and (c) on the scales below.
Answer
a.1250
b.1325
c.1475
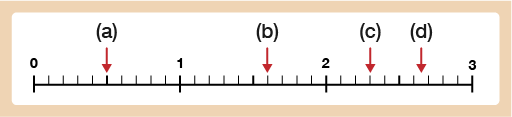
Read the values for (a), (b), (c) and (d) on the scales below.
Answer
a.0.5
b.1.6
c.2.3
d.The arrow is pointing to halfway between 2.6 and 2.7 so the reading is 2.65.
Now have a go at reading the scales on the different instruments of measure.
Activity 11: Measuring instruments
How much water is left in the bottle, to the nearest 50 millilitres (ml)?
Answer
The bottle holds 1 litre of liquid in total. There are 10 large steps marked on the bottle so each one marks 100 ml (1 litre = 1000 ml and 1000 ÷ 10 = 100).
Halfway between each large step there is a small step so each of these marks off 50 ml.
This means there is 250 ml of water left in the bottle to the nearest 50 ml.
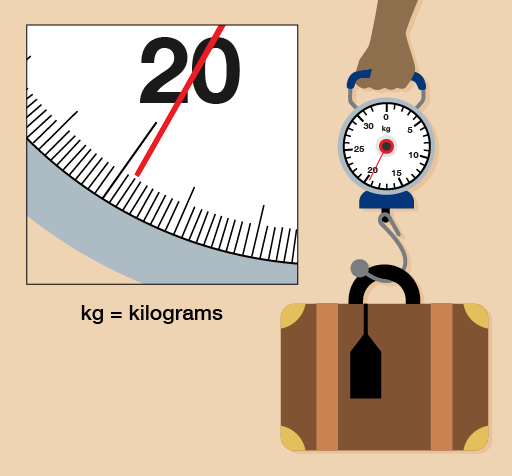
Sara weighs her case using a set of luggage scales. She has a weight limit of 21 kg. How much more can she pack to the nearest 100 grams?
Answer
To answer this question you need to remember that 1 kg = 1000 g.
The scale is numbered at every 1 kg interval and there are 10 steps between each numbered interval, so each step marks 0.1 kg (1 ÷ 10 = 0.1). You could also think of each marker being 100 g (0.1 kg = 100 g).
The arrow is almost at 19.8 kg (19 800 g). If Sara has a weight limit of 21 kg then:
21 kg − 19.8 kg = 1.2 kg (21 000 g − 19 800 g = 1200 g)
Sara can pack another 1.2 kg (or 1200 g) worth of luggage.
Simon needs to weigh out 4 kg of potatoes. Looking at the reading on the scale, how many more grams of potatoes does he need to add to make 4 kg?
Answer
As with Question 2, you need to remember that 1 kg = 1000 g.
The scale is numbered at every 1 kg interval and there are 10 steps between each numbered marker so each step marks 0.1 kg (1 ÷ 10 = 0.1). You could also think of each step being 100 g (0.1 kg = 100 g).
The arrow is pointing to 3.8 kg (or 3800 g).
If Simon needs 4 kg (4000 g) of potatoes then he needs to weigh out another 200 g.
Hopefully you will be feeling confident at reading scales on measuring devices now which leads you nicely onto the next section which looks at conversion scales.