2.2 Wave speed, amplitude and displacement

The interaction of a wind over the surface of water to produce waves is complex. On the surface of deep water the wave speed of typical waves can be modelled as

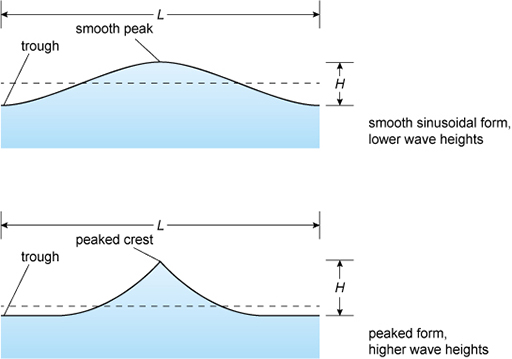
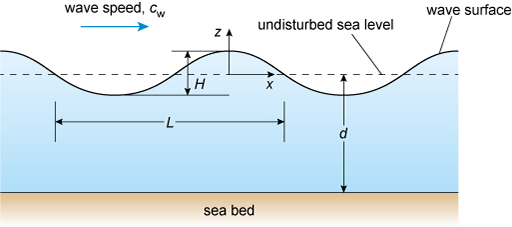
where is the wavelength from peak to peak between two waves following each other and is the acceleration due to gravity. The peak is the highest point of the wave, and is also known as the crest. Thus the wave speed is greater for longer wavelengths. Consequently a swell may comprise long and fast waves, which can also be very high if the initiating wind speed itself is both high and sustained for a significant time. The height, , of a wave is taken to be the distance from the lowest level of the surface to the top of the wave. The lowest level is called the trough. The shape of a wave – its cross section or side view – depends upon its height and wavelength. At lower heights, it tends to be sinusoidal, so the amplitude of this type of wave will be half the height from trough to crest.

Higher waves tend to have a narrower crest and a wider and shallower trough, as sketched in Figure 12.

At a value of the crests become more pronounced and sharp-edged in profile and the top edges break into foaming white water (white horses). This foaming dissipates energy, which effectively stops further growth in height, meaning that the ratio stays at a maximum value of .

Figure 12 Cross sections of wave profiles

Show description|Hide description

This shows 2 waves in cross-section. The upper diagram shows one cycle of a sinusoidal wave (same shape as a sine curve), from a trough to the curved peak to the next trough. The distance between the troughs is L and vertical distance from trough to peak is H. A horizontal line passes halfway between the 2 peaks. The graph label is ‘sinusoidal form, lower wave heights’.

The lower diagram has a different shape. From the trough on the left, the wave has a steady height for about one third of L, then rises diagonally upwards to a pointed peak, then falls to a second trough on the right by sloping down and being flat. H is the distance from trough to peak again and the horizontal line is only a small distance above the troughs. The label is ‘peaked form, higher wave heights’.

Figure 12 Cross sections of wave profiles

The breaking of waves is of course most evident in shallow water at the beach. Once the depth of water has reduced to about , the shape of the wave profile alters again. If the slope of the beach is small (e.g. less than about 1 in 30 or 3.3%) the wave will break progressively as it rolls in, and the water itself does travel along in this case. If the slope is much greater, the wave is effectively slowed down and cannot adjust; instead, it becomes unstable, growing in height and then breaking by plunging over in a dramatic fashion. This still contains a lot of energy and can impart high forces on anything in its path. Even a non-breaking wave can cause large forces owing to the energy it contains, as the speed causes drag forces on anything it flows past.

A typical wave can be modelled quite easily. Figure 13 shows a wave of sinusoidal form with a relatively small surface displacement amplitude  in comparison to the wavelength and depth  of the water. The sea bed is assumed to be flat and smooth (with negligible friction), and there is a steady series of waves flowing to the right with speed . The wave depth is , which in this model will be twice the amplitude. The wave periodic time, , is the time taken for one complete wavelength to pass through and is given by

Figure 13 Cross section of a sinusoidal wave profile

Show description|Hide description

This shows 2 complete cycles of a sinusoidal wave on the surface of water. There is a horizontal line halfway between peaks and troughs, the flat sea surface. L is the distance between 2 similar points e.g. 2 peaks and H is the vertical distance from peak to trough. d is the depth from the sea bed to flat sea surface. Waves move from the left with wave speed c subscript w. The coordinate axis is x positive to the right and z positive vertically upwards.

Figure 13 Cross section of a sinusoidal wave profile

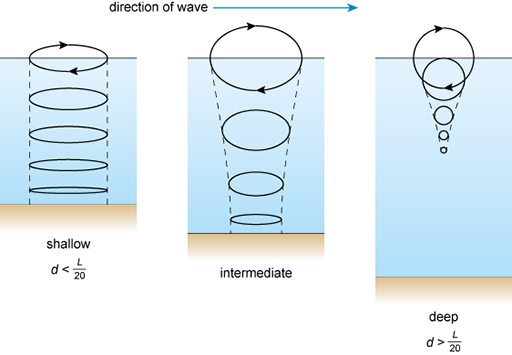
As mentioned above, each water particle will move in an approximately circular orbit as the wave disturbance passes through. Figure 14 shows the shapes of an individual water particle orbits for shallow, intermediate depth and deep water in schematic form; the relative sizes are not to scale. In shallow water, the orbit is elliptical in cross section and reaches to the sea bed. In the intermediate depth, the orbit is more circular, and in deep water the orbit is completely circular and does not extend to the sea bed.

Figure 14 Wave water particle orbits (not to scale)

Show description|Hide description

This shows the paths followed by wave water particles for three regimes. In each case, the wave moves from left to right.

Left figure: shallow water, d less than L divided by 20. The path of the surface is elliptical and clockwise. The height of each ellipse is less than length. The height of the ellipse for deeper paths decreases with depth (the ellipses get flatter), though the length of each ellipse remains constant with depth. The ellipses are shown getting close to the sea bed.

Middle: intermediate. The path of the surface is elliptical and clockwise. The height of each ellipse is less than length. The height and length of depth of each ellipse decrease with depth. The ellipses are shown getting close to the sea bed.

Right figure: deep water, d greater than L divided by 20. The path is circular and clockwise. The radius of these paths decreases with depth and disappear completely a long way above the sea bed.

Figure 14 Wave water particle orbits (not to scale)

Generally at a water depth equivalent to half the wave length, , the amplitude of wave motion is barely 4% of that at the surface. This forms a useful rule of thumb in defining a ‘deep water’ wave. Assuming a deep water situation, the wave motion of an individual particle of water as a wave passes is near enough circular. Taking a stationary reference axis set at the flat sea level, as the depth increases with , the wave motion amplitude reduces by a factor of , where numerically will be negative.

In other words, if is the surface amplitude and is the amplitude at depth (where is a negative number) then

If the radius of the circular motion is , the particle speed will be given by (as with any circular motion), and its acceleration will be

where is the radian circular frequency. Again, as with all circular orbiting motion

and

which is a rearranged version of Equation 13.