2 Scale of the Universe
Our bodies, in common with all material on the Earth, the planets of our Solar System, the Sun, stars and galaxies are composed of what we call matter. Much of the matter in and among the stars is composed of atoms and molecules that are familiar here on Earth. An atom is made up of particles called electrons which occupy a cloud-like structure around a central nucleus composed of protons and neutrons. The electrical attraction between negatively charged electrons and positively charged protons holds the atom together. A chemical element is defined by the number of protons in the nucleus. Hydrogen has one proton, helium has two and so on. A molecule is a group of two or more atoms (see Figure 2).
Many of the molecules in the human body are extremely complex combinations of atoms of different elements, but the simplest atom, hydrogen is the most common chemical element in the Universe, and helium is the second most common.
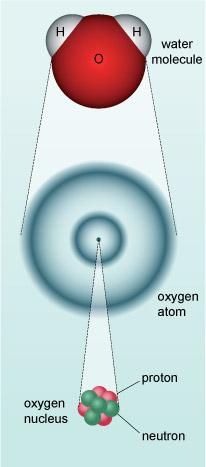
Atoms are among the smallest objects that are found in the Universe (individual hydrogen atoms are abundant in the interstellar medium - the space between the stars). Everyday units for length (such as metres) are just as inappropriate for these tiny objects as they are for defining the vast distances between stars.
When measuring the scale of the Universe it's necessary to consider the smallest and largest objects and distances and how they're defined. The physical quantity of interest is length (it may be the diameter of an object or its distance from us).
Units, numbers and physical quantities
Much of astronomy concerns quantities such as distances, masses, temperatures, etc. In all of these cases, units of measurement are important. Physical quantities are generally the result of multiplying together a number and a unit of measurement. Thus a distance such as 5.2 metres is really the result of multiplying the number 5.2 by the unit of distance known as the metre. There are many units of measurement in common use, so, whenever you quote the value of a physical quantity, you should always take care to include the unit as well as the number multiplying that unit. It is no use being told that a distance is 5.2 if you don't know whether that means 5.2 centimetres or 5.2 metres. The unit is just as important as the number.
In scientific work there are several internationally agreed conventions for the definition of units and the way in which units should be used and represented when writing down the values of physical quantities. The most widely adopted system of units is known as SI, which stands for Système International. This is based on seven carefully defined units that include the metre (for length), the second (for time) and the kilogram (for mass). The other four base units relate to luminous intensity (i.e. brightness), quantity of matter, electric current and temperature.
The SI unit of temperature is called the kelvin (signified by the abbreviation K and not °K). A difference of 1 K is the same as a difference of 1 °C but the Kelvin scale starts from a different zero point. 0 °C corresponds to the temperature at which water freezes (at the Earth's atmospheric pressure). 0 K, which is equal to −273.15 °C, corresponds to absolute zero where, in the classical theory of matter, all motion of atoms ceases. Both scales are used in scientific literature. The Celsius scale, which is generally used in everyday life, is more commonly used for biological environments, whereas the Kelvin scale is used for the wider temperature ranges found in astronomy.
The recognised abbreviations for the metre, the second and the kilogram are m, s and kg, respectively. Abbreviated units should always be written in the singular form, i.e. 5.2 m, rather than 5.2 ms, since that might be misinterpreted as 5.2 × 1 m × 1 s or as 5.2 milliseconds, which is abbreviated to 5.2 ms. When writing units in full, for example as the result of a calculation, the singular should also be used (e.g. 5.2 metre rather than 5.2 metres). It is, however, acceptable to use the plural when expressing quantities in text to maintain correct grammar, as in the following paragraph.
In calculations, units should be treated in the same way as numbers. For example, speed is distance travelled divided by time taken, so the unit of speed is the unit of distance (metre) divided by the unit of time (second). For example, the result of dividing 6.0 m by 3.0 s is 2.0 m/s, which can be read as 2.0 metres per second.
Units that result from combining the base units are called derived units. The most common derived units are sometimes given their own names and symbols. Examples are the joule (J; unit of energy) and the watt (W; unit of power, which is energy per unit time or J/s).
The size of an atom is about one-ten-billionth of a metre, and the nucleus of that atom is around a hundred thousand times smaller still! Clearly some different units for distance are needed that are more appropriate for the very small and very large. One way to do this is to use units that are appropriate for a given scale. For example, the size of an atom is better described by a unit that is one-ten-billionth of a metre in size called an ångström (Å), whereas distances to stars can be measured in light-years (ly).
You have already been introduced to the light-year.
If light travels at 300 million metres in one second, how many metres are there in a light-year?
The number of seconds in a year is about (365.25 days) × (24 hours in a day) × (60 minutes in an hour) × (60 seconds in a minute), which equals over 30 million seconds (31 557 600 to be precise). So light will travel 300 000 000 × 31 557 600 = 9467 280 000 000 000 metres in a year.
You can see that 1 ly is easier to write than 9467 280 000 000 000 m! In fact professional astronomers use a different unit to measure the distance of stars, the parsec (pc), which is about 3.26 ly.
Ångströms, metres and parsecs cover an enormous range of sizes, and are ideal for measuring at atomic, human and stellar distance scales respectively. However, an even smaller unit than an ångström is needed to describe the sizes of atomic nuclei, and an even larger unit than the parsec for distances to other galaxies. Rather than invent new units every time we need to describe a certain scale, the SI unit of length, the metre, can be used. But how?
Very large and very small numbers
The SI unit of length is the metre. If you want to measure something that is typically 1000 times smaller or larger then you can use the familiar units the millimetre and kilometre respectively. So, using the same process, you could have units that are progressively 1000 times smaller or larger to reach any scale that's needed. The lists below show how:
So attometres would be useful for measuring atomic nuclei and petametres for measuring the distances to nearby stars. Figure 3 shows how these units relate to the scale of the Universe.
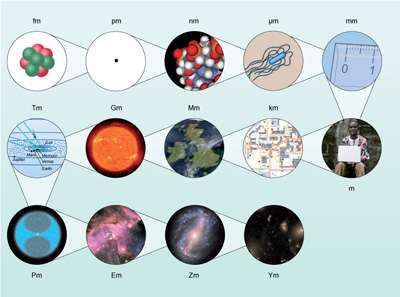
Most of these units will sound unfamiliar, not just because they refer to scales that we do not come across in our daily lives. Astronomy is an ancient science and certain non-SI units are commonly used instead, such as the ångström and parsec. Within our Solar System, distances are measured in units of the average distance of the Earth from the Sun, called the astronomical unit (AU). The rest of this course looks at the objects that can be observed in the Universe, starting with our own planetary system and the star that supports life on Earth, and then moving out to stars and galaxies.