2.4 Models as part of systems work
Thinking systemically involves identifying systems relevant to some situation, and models are invariably used as part of this process. An example of this forms part of Checklands' Soft Systems Methodology (SSM) (Checkland, 1981). One aspect of this methodology concerns the formulation of a root definition of some system that is relevant to the situation of interest and the construction of a conceptual model of this system. The root definition is a concise, verbal description of what a system does, or is supposed to do. The conceptual model then consists of a series of verbs, which define the activities essential to achieve whatever it is that the system is required to do.
So, to take an extremely naive and simple example, let's consider the situation in which I find myself as I write this, in the room that I use as an office at home. It is freezing outside, and my room is not at what I consider to be a very comfortable temperature. I can switch on an electric heater, but then if I leave the room for a period, with the heater running, it may be too hot when I get back, and the window will have to be opened, wasting all that expensive electricity! Pretty clearly, there is a need for a system to control the temperature of the room at or near a desired level. From general knowledge and experience in the UK, we probably have a mental model of such a system, perhaps comprising a radiator, plumbing, a boiler, room thermostat, etc. This would actually be just one physical realisation of such a system, and would only be appropriate to particular circumstances. It might not, for example, be relevant if my room only has an electricity supply, and it would also not be relevant to a climate such as southern Europe, or parts of the USA, where cooling, rather than heating, might be needed. Constructing a conceptual model of the system required by the root definition forces us to consider the fundamental activities that such a system must carry out, independently of any particular physical realisation of that system. It is purely a conceptual model, which can underlie all sorts of different physical realisations. Checkland (1981) describes the distinction thus:
… the conceptual model is a statement of what is logically and necessarily implied by the [root] definition. It is not a recommendation of what ought to exist nor of what does exist in the real [sic] situation.
So, in this case, my conceptual model of the system would require it to involve the following activities:
-
know the desired temperature
-
sense the current temperature
-
compare the current and desired temperatures
-
use energy (to change the temperature) if the desired and current temperatures are different.
From general knowledge, you should be able to work out that if any of these activities is missing, then the system cannot operate as required. The model allows for both heating and cooling, and only specifies that a source of energy is needed to fulfil its activities.
This type of model relies on the use of verbs (‘know, sense, etc.’) but can also involve diagrams that show the logical or sequential relationship between the activity verbs. So, in the case of the temperature control system, the action of comparing can only occur if both the temperatures are known, and using energy only occurs as a result of the comparison. So the verbs need to be linked logically as shown in Figure 6.
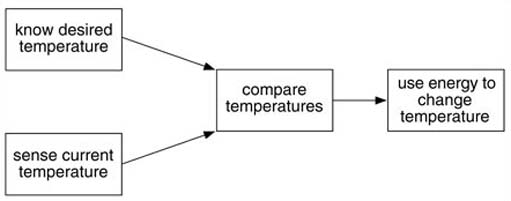
While this example is relatively trivial and straightforward, it does illustrate some of the important aspects of both this particular modelling method, and the process in general. The conceptual model is related to, but does not necessarily represent, any existing system. In this case, it is at a very abstract level, and it draws on knowledge of basic physics and engineering to set up the essential characteristics of a system that needs to be designed. So the model sets a fundamental minimum set of activities that has to be present, but does not constrain the physical implementation at this stage. Obviously, if we wanted to go on to design and implement an actual system for my room, other aspects of the real situation would have to be incorporated, but the fundamental model would still be valid. This is a characteristic of the models most useful in systems work, which will generally operate in a large number of contexts and need not be tied to specific situations. In this pack we will be examining the quantitative models that have this property.
