Find out more about The Open University's Mathematics courses.
These rules define how a tile can be subdivided into a group of smaller tiles. Tilings are constructed by starting with a single tile and iteratively applying these rules until the required tiling is achieved. The rule for the Penrose rhombus tiling can be seen below along with a tiling produced by starting with a thick rhombus and applying substitution rules four times.
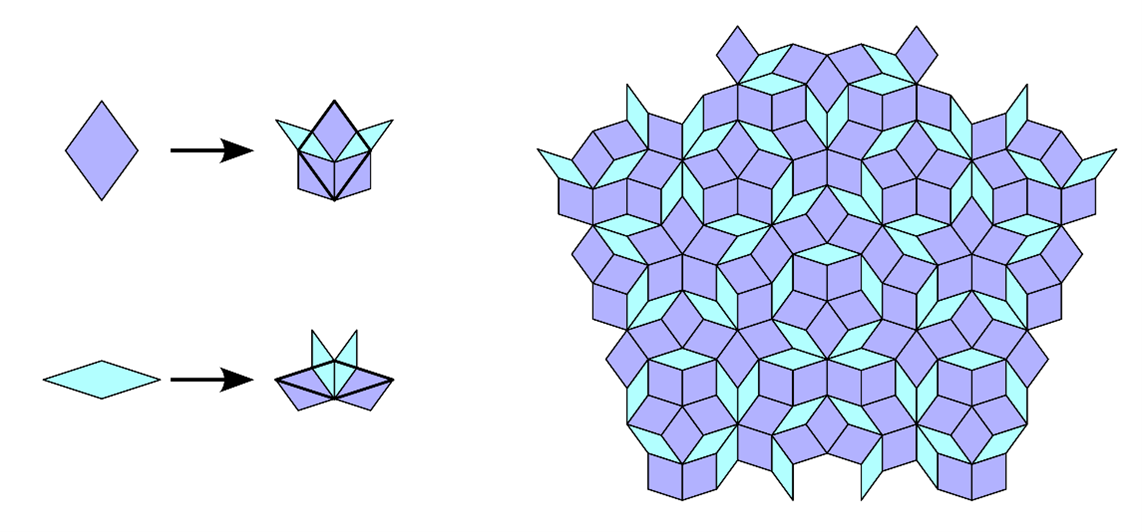
Mathematicians at The Open University are investigating tilings produced by applying random substitution rules. The tiling above has one rule and so the resulting tiling will always be the same after applying the rule four times. This short game shows how distinct tilings can be produced just by applying two rules in a random sequence. The aim of the game is to replicate a target tiling by working out the random sequence of rules that have been applied. Click on the tile formations within the game to apply them, if it matches the target tiling after three substitutions, you win. The second level is tricky, you will need to think ahead.
The Substitution game
[Link to the game to be added here].
Instructions
- Study the target tiling
- Click on the first rule you think was applied
- Click on the second rule
- Click on the third rule
- If the game tiling matches the target tiling, click on “Next level”
- If the game tiling does not match the target tiling, click on “Restart".







Rate and Review
Rate this activity
Review this activity
Log into OpenLearn to leave reviews and join in the conversation.
Activity reviews