Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Introduction to complex analysis
Introduction to complex analysis

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

1.3 Non-differentiability

In Theorem 1 you saw that differentiability implies continuity. An immediate consequence of this is the following test for non-differentiability.

Strategy A for non-differentiability

If f is discontinuous at alpha, then f is not differentiable at alpha.

Example 4

Show that there are no points of the negative real axis at which the function f of z equals Square root of z is differentiable.

Solution

The function f of z equals Square root of z is discontinuous at all points of the negative real axis. It follows that there are no points of the negative real axis at which f is differentiable.

Exercise 6

Show that there are no points of the negative real axis at which the principal logarithm function

Log of z equals log of absolute value of z plus i times Arg of z

is differentiable.

Answer

The function Arg is discontinuous at each point of the negative real axis. It follows that Log is discontinuous at each point of the negative real axis, and hence that there are no points on it at which Log is differentiable.

The converse of Theorem 1 is not true; if a function is continuous at a point, then it does not follow that it is differentiable at the point. A particularly striking illustration of this is provided by the modulus function f of z equals absolute value of z. This is continuous on the whole of double-struck cap c and yet, as you will see, it fails to be differentiable at any point of double-struck cap c.

Since f of z equals absolute value of z is continuous, Strategy A cannot be used to show that f is not differentiable at a given point alpha. Instead we return to the definition of derivative and show that the difference quotient for f fails to have a limit.

In general, if the domain cap a of a function f contains alpha as one of its limit points, then the existence of the limit

lim over z right arrow alpha of f of z minus f of alpha divided by z minus alpha

means that for each sequence left parenthesis z sub n right parenthesis in cap a minus alpha that converges to alpha,

lim over n right arrow normal infinity of f of z sub n minus f of alpha divided by z sub n minus alpha

exists, and has a value that is independent of the sequence left parenthesis z sub n right parenthesis.

So, if two such sequences left parenthesis z sub n right parenthesis and left parenthesis z sub n super prime right parenthesis can be found for which

lim over n right arrow normal infinity of f of z sub n minus f of alpha divided by z sub n minus alpha not equals lim over n right arrow normal infinity of f of z sub n super prime minus f of alpha divided by z sub n super prime minus alpha comma

then f cannot be differentiable at alpha.

In the next example, you will see that f of z equals absolute value of z is not differentiable at zero. This result should not surprise you because the real modulus function is not differentiable at zero. Indeed, the proof is identical to that of the real case.

Example 5

Prove that f of z equals absolute value of z is not differentiable at 0.

Solution

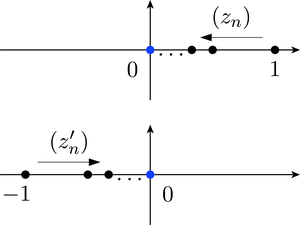
We need to find two sequences left parenthesis z sub n right parenthesis and left parenthesis z sub n super prime right parenthesis that converge to 0 which, when substituted into the difference quotient, yield sequences with different limits. A simple choice is to pick sequences left parenthesis z sub n right parenthesis and left parenthesis z sub n super prime right parenthesis that approach 0 along the real axis: one from the right, and one from the left, as shown in Figure 4.

Described image
Figure 4 Sequences converging to zero from the right and left
Show description|Hide description

This figure consists of two copies of the complex plane, one above the other. The upper copy shows on the positive real axis a sequence of points that approach zero from the right. The origin is labelled zero and marked with a solid blue dot. The point 1 is labelled, and the first three points in the sequence, starting with 1, are marked with solid black dots. An ellipsis to the left of the third point (one third) indicates that the sequence continues indefinitely getting closer to zero. A horizontal arrow above the real axis, between zero and 1, points from right to left. Above it is the label, open bracket, z sub n, close bracket. The lower copy of the complex plane shows on the negative real axis a sequence of points that approach zero from the left. The origin is labelled zero and marked with a solid blue dot. The point negative 1 is labelled, and the first three points in the sequence, starting with negative 1, are marked with solid black dots. An ellipsis to the right of the third point (negative one third) indicates that the sequence continues indefinitely getting closer to zero. A horizontal arrow above the negative real axis, between negative 1 and zero, points from left to right. Above it is the label, open bracket, z prime sub n, close bracket.

Figure 4 Sequences converging to zero from the right and left

There is no point in picking sequences that are more complicated than they need to be, so let z sub n equals one solidus n, n equals one comma two comma ellipsis. Then

equation sequence part 1 lim over n right arrow normal infinity of absolute value of z sub n minus absolute value of zero divided by z sub n minus zero equals part 2 lim over n right arrow normal infinity of one solidus n divided by one solidus n equals part 3 one full stop

Now let z sub n super prime equals negative one solidus n, n equals one comma two comma ellipsis. Then

equation sequence part 1 lim over n right arrow normal infinity of absolute value of z sub n super prime minus absolute value of zero divided by z sub n super prime minus zero equals part 2 lim over n right arrow normal infinity of one solidus n divided by negative one solidus n equals part 3 negative one full stop

Since the two limits do not agree, the difference quotient does not have a limit as z tends to 0. It follows that f of z equals absolute value of z is not differentiable at 0.

The next exercise asks you to extend the method used in Example 5 to show that f of z equals absolute value of z is not differentiable at any point of double-struck cap c.

Exercise 7

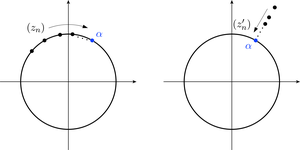
Let alpha be any non-zero complex number, and consider the circle through alpha centred at the origin. By choosing one sequence left parenthesis z sub n right parenthesis that approaches alpha along the circumference of the circle, and another sequence left parenthesis z sub n super prime right parenthesis that approaches alpha along the ray from zero through alpha, prove that f of z equals absolute value of z is not differentiable at alpha.

Described image
Show description|Hide description

This figure consists of two copies of the complex plane, arranged side by side. The axes are not labelled. The left-hand copy shows a circle centred at the origin. An arbitrary point on the circle in the upper-right quadrant is labelled alpha and marked with a solid blue dot. A sequence of points on the circumference starts in the upper-left quadrant and approaches the point alpha at decreasing intervals. The first four points in the sequence are marked with solid black dots. An ellipsis between the fourth point and the point alpha indicates that the sequence of points continues indefinitely getting closer to alpha. Above the sequence of points is a curved arrow pointing from left to right. It is labelled: open bracket, z sub n, close bracket. The right-hand copy of the complex plane shows the same circle centred at the origin, and the same arbitrary point alpha on the circle is labelled and marked with a solid blue dot. A sequence of points outside the circle approaches the point alpha at decreasing intervals along the normal to the circle at alpha. The first three points in the sequence are marked with solid black dots. An ellipsis between the third point and the point alpha indicates that the sequence of points continues indefinitely getting closer to alpha. An arrow directed towards alpha is drawn outside the circle parallel to the sequence of points. It is labelled: open bracket, z prime sub n, close bracket.

Answer

Let z sub n equals alpha times exp of i solidus n, n equals one comma two comma ellipsis. Then left parenthesis z sub n right parenthesis tends to alpha along the circumference of the circle, and

equation sequence part 1 lim over n right arrow normal infinity of absolute value of z sub n minus absolute value of alpha divided by z sub n minus alpha equals part 2 lim over n right arrow normal infinity of absolute value of alpha minus absolute value of alpha divided by z sub n minus alpha equals part 3 zero full stop

Now let z sub n super prime equals alpha times left parenthesis one plus one solidus n right parenthesis, n equals one comma two comma ellipsis. Then left parenthesis z sub n super prime right parenthesis tends to alpha along the ray from zero through alpha, and

multiline equation row 1 Blank equation sequence part 1 lim over n right arrow normal infinity of absolute value of z sub n super prime minus absolute value of alpha divided by z sub n super prime minus alpha equals part 2 lim over n right arrow normal infinity of absolute value of alpha times left parenthesis one plus one solidus n right parenthesis minus absolute value of alpha divided by alpha times left parenthesis one plus one solidus n right parenthesis minus alpha equals part 3 absolute value of alpha divided by alpha full stop Blank

Since absolute value of alpha solidus alpha not equals zero for alpha not equals zero, these two limits do not agree. It follows that f of z equals absolute value of z is not differentiable at alpha not equals zero.

The modulus function illustrates an important difference between real and complex differentiation. When the modulus function is treated as a real function, the limit of its difference quotient has to be taken along the real line. But when treated as a complex function, the limit of the difference quotient is required to exist however the limit is taken. This explains why the real modulus function is differentiable at all non-zero real points, whereas the complex modulus function fails to be differentiable at any point of double-struck cap c. More generally, it shows that complex differentiability is a much stronger condition than real differentiability.

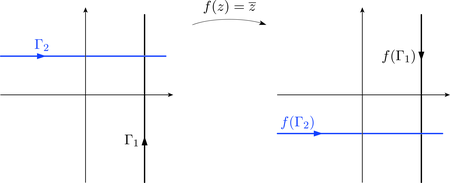
In Exercise 7 you were asked to prove that the modulus function fails to be differentiable by observing that its behaviour along the circumference of a circle centred at 0 is different from its behaviour along a ray. Similar observations can be applied to other functions. For example, in the next exercise you may find it helpful to notice that directions of paths parallel to the imaginary axis are reversed by the function f of z equals z macron, whereas directions of paths parallel to the real axis are left unchanged (Figure 5).

Described image
Figure 5 Images of horizontal and vertical lines under f of z equals z macron
Show description|Hide description

This figure consists of two copies of the complex plane, arranged side by side. The axes are not labelled. On the left-hand diagram, a bold vertical line, drawn in black, passes through an arbitrary point on the positive horizontal axis. It is marked with a direction arrow pointing upwards, and labelled capital gamma sub 1. A bold horizontal line, drawn in blue, passes through an arbitrary point on the positive vertical axis. It is marked with a direction arrow pointing to the right, and labelled capital gamma sub 2. The two bold lines intersect at right angles in the upper-right quadrant. Between the two copies of the complex plane is a curved horizontal arrow pointing from left to right. It is labelled f of z equals z bar. On the right-hand diagram, a bold vertical line, drawn in black, passes through the same arbitrary point on the positive horizontal axis. It is marked with a direction arrow pointing downwards, and labelled f of capital gamma sub 1. A bold horizontal line, drawn in blue, passes through a point on the negative vertical axis. (This point is the same distance below the origin as the point used on the vertical axis in the left-hand diagram was above it.) The horizontal line is marked direction arrow pointing to the right, and labelled f of capital gamma sub 2. The two bold lines intersect at right angles in the lower-right quadrant.

Figure 5 Images of horizontal and vertical lines under f of z equals z macron

Exercise 8

Show that there are no points of double-struck cap c at which the complex conjugate function f of z equals z macron is differentiable.

Answer

Let alpha be an arbitrary complex number. Directions of paths parallel to the imaginary axis through alpha are reversed by f, while directions of paths parallel to the real axis are not. This suggests looking at the sequences z sub n equals alpha plus one solidus n and z sub n super prime equals alpha plus i solidus n, n equals one comma two comma ellipsis.

First let z sub n equals alpha plus one solidus n; then

multiline equation row 1 lim over n right arrow normal infinity of zn macron minus alpha macron divided by z sub n minus alpha equals lim over n right arrow normal infinity of left parenthesis right parenthesis solidus solidus plus plus alpha one n macron minus alpha macron divided by left parenthesis alpha plus one solidus n right parenthesis minus alpha row 2 Blank equation sequence part 1 equals part 2 lim over n right arrow normal infinity of one solidus n divided by one solidus n equals part 3 one full stop

Now let z sub n super prime equals alpha plus i solidus n; then

multiline equation row 1 lim over n right arrow normal infinity of zn prime macron minus alpha macron divided by z sub n super prime minus alpha equals lim over n right arrow normal infinity of left parenthesis right parenthesis solidus solidus plus plus alpha in macron minus alpha macron divided by left parenthesis alpha plus i solidus n right parenthesis minus alpha row 2 Blank equation sequence part 1 equals part 2 lim over n right arrow normal infinity of negative i solidus n divided by i solidus n equals part 3 negative one full stop

Since these two limits do not agree, and since alpha is arbitrary, it follows that there are no points of double-struck cap c at which f of z equals z macron is differentiable.

For some functions f, you may be able to find a sequence left parenthesis z sub n right parenthesis that converges to alpha for which the sequence

w sub n equals f of z sub n minus f of alpha divided by z sub n minus alpha comma n equals one comma two comma ellipsis comma
Equation label: (equation 1)

is divergent. In such cases, there is no need to look for a second sequence.

Example 6

Show that the function f of z equals Square root of z is not differentiable at 0.

Solution

Strategy A cannot be used here, since f is continuous at 0. Instead we look for a sequence left parenthesis z sub n right parenthesis that converges to zero for which the sequence 1 (above) is divergent. To make the square roots easy to handle, let z sub n equals one solidus n squared, n equals one comma two comma ellipsis. Then

equation sequence part 1 f of z sub n minus f of zero divided by z sub n minus zero equals part 2 Square root of one solidus n squared minus Square root of zero divided by one solidus n squared minus zero equals part 3 one solidus n divided by one solidus n squared equals part 4 n full stop

This sequence tends to infinity, and is therefore divergent. It follows that f is not differentiable at 0.

The methods exemplified above for showing that a function is not differentiable at a given point can be summarised as follows.

Strategy B for non-differentiability

To prove that a function f is not differentiable at alpha, apply the strategy for proving that a limit does not exist to the difference quotient

f of z minus f of alpha divided by z minus alpha full stop

If you think that a given function is not differentiable, then you should try to apply Strategy A or Strategy B. A third strategy for proving that f is not differentiable at a point will appear in Section 2.1. If, on the other hand, you think that the function is differentiable, then you should try to find the derivative.

Exercise 9

Decide whether each of the following functions is differentiable at i. If it is, then find its derivative at i.

  • a.f of z equals Re of z

  • b.f of z equals sum with 3 summands two times z squared plus three times z plus five

  • c.f of z equals case statement case 1column 1 comma z comma less than less than of ReRez zero case 2column 1 comma four comma greater than or equals greater than or equals of ReRez zero

Answer

  • a.The fact that Re of z is constant along the imaginary axis, but variable parallel to the real axis, suggests that Re is not differentiable at i (or anywhere else, for that matter). It also suggests looking at the sequences z sub n equals i plus i solidus n and z sub n super prime equals i plus one solidus n, n equals one comma two comma ellipsis.

    First let z sub n equals i plus i solidus n; then

    multiline equation row 1 lim over n right arrow normal infinity of Re of z sub n minus Re of i divided by z sub n minus i equals lim over n right arrow normal infinity of Re of i plus i solidus n minus Re of i divided by left parenthesis i plus i solidus n right parenthesis minus i Blank row 2 Blank equation sequence part 1 equals part 2 lim over n right arrow normal infinity of zero divided by i solidus n equals part 3 zero full stop Blank

    Now let z sub n super prime equals i plus one solidus n; then

    multiline equation row 1 lim over n right arrow normal infinity of Re of z sub n super prime minus Re of i divided by z sub n super prime minus i equals lim over n right arrow normal infinity of Re of i plus one solidus n minus Re of i divided by left parenthesis i plus one solidus n right parenthesis minus i Blank row 2 Blank equation sequence part 1 equals part 2 lim over n right arrow normal infinity of one solidus n divided by one solidus n equals part 3 one full stop Blank

    Since these two limits do not agree, it follows that Re is not differentiable at i.

  • b.f is a polynomial function, so f super prime of z equals four times z plus three for all z element of double-struck cap c. Thus f super prime of i equals three plus four times i.

  • c.f is not differentiable at i, since it is not continuous at i.