Session 2: Integration

Introduction to integration

This session introduces complex integration, an important concept which gives complex analysis its special flavour. We spend most of this session setting up the complex integral, deriving its main properties, and illustrating various techniques for evaluating it.

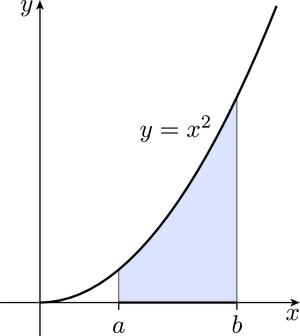
To define the integral of a complex function, it is instructive to first consider real integrals, such as

where , which represents the area of the shaded part of Figure 1 (for ). We can express this equation in words by saying that

Figure 1 Area under the graph of between and 

Show description|Hide description

The figure shows Cartesian axes labelled x and y and is concentrated in the upper-right quadrant. The graph of y equals x squared is drawn and labelled. Points a and b are labelled on the positive x-axis with a being nearer the origin. The line joining these two points on the x-axis is a bold line. The two points have vertical lines drawn to meet the parabola y equals x squared. The area under the graph and above the positive x-axis is shaded.

Figure 1 Area under the graph of between and 

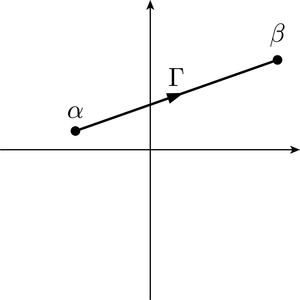
Suppose now that we wish to integrate the complex function between two points and in the complex plane. To do this, we first need to specify exactly how to get from to . We could, for example, choose the line segment from to , as shown in Figure 2. It turns out (as you will see later) that if we make this choice, then

We write this as

Figure 2 Line segment from to

Show description|Hide description

The figure shows the complex plane with unlabelled axes and concentrated in the upper half-plane. There is a point alpha in the upper-left quadrant marked with a solid dot and a point beta in the upper-right quadrant also marked with a solid dot. The point beta is higher than alpha and further to the right than alpha is to the left of the origin. A bold line joins the two points and is marked with an arrow in the direction from alpha to beta and is labelled capital gamma.

Figure 2 Line segment from to

But there are many other paths in the complex plane from to , which raises the following question. Do we get the same answer if we integrate the function along a different path from to ?

In order to address this question, we first need to explain exactly what it means to ‘integrate a function along a path’. This is one of the objectives of Section 1, where we briefly review the Riemann integral from real analysis, and then use similar ideas to construct the integral of a complex function along a path in the complex plane. We will see that if is a complex function that is continuous on a smooth path in the complex plane, then the integral of along , denoted by , is given by the formula

We can evaluate this integral by splitting into its real and imaginary parts and , and evaluating the resulting pair of real integrals:

Section 2 begins with this definition of the integral of a complex function along a smooth path, and then extends the idea to allow integration along a contour – a finite sequence of smooth paths laid end to end.

In Section 3 we prove the Fundamental Theorem of Calculus, which shows that integration and differentiation are essentially inverse processes. From this result it follows that the integral of along any contour from  to is .

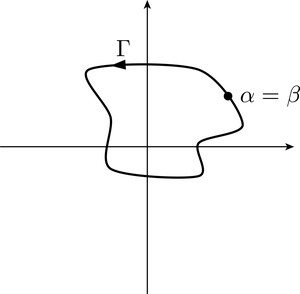
We will need to be careful about how we apply results such as the Fundamental Theorem of Calculus. For example, suppose that the endpoints and of coincide, as illustrated in Figure 3. Then

In this case, the integral of the function along is .

Figure 3 Contour with initial point and final point coinciding

Show description|Hide description

The figure shows the complex plane with unlabelled axes. There is a closed contour with irregular shape marked with an arrow in an anticlockwise direction and labelled capital gamma. The contour covers all four quadrants and has the point alpha equals beta marked with a solid dot.

Figure 3 Contour with initial point and final point coinciding

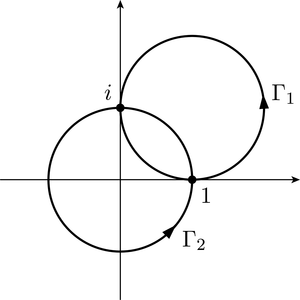
Consider now the function . We will see later in Example 4 that if we integrate along the smooth paths and shown in Figure 4, where and are circles traversed once anticlockwise, then

The reason for this difference will become apparent in Section 3.

Figure 4 Circular paths and

Show description|Hide description

The figure shows the complex plane with unlabelled axes. There are two circles drawn both with radius 1. The first is in the upper-right quadrant with centre 1 plus i. and is labelled with an arrow in an anticlockwise direction marked as capital gamma sub 1. The second has the origin as its centre and is labelled with an arrow in an anticlockwise direction marked as capital gamma sub 2. The points i and 1 are marked as solid dots and both circles pass through these points.

Figure 4 Circular paths and