Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Introduction to complex analysis
Introduction to complex analysis

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

1.5 A geometric interpretation of derivatives

As we mentioned in this session’s introduction, the derivative of a real function is often pictured geometrically as the gradient of the graph of the function. This interpretation is useful in real analysis, but it is of little use in complex analysis, since the graph of a complex function is not two-dimensional.

Fortunately, there is another way of interpreting derivatives that works for complex functions.

If a complex function f is differentiable at a point alpha, then any point z close to alpha is mapped by f to a point f of z close to f of alpha.

Indeed, by the Linear Approximation Theorem,

f of z equals sum with 3 summands f of alpha plus left parenthesis z minus alpha right parenthesis times f super prime of alpha plus e of z comma

where e of z solidus left parenthesis z minus alpha right parenthesis right arrow zero as z right arrow alpha. So if f super prime of alpha not equals zero, then, to a close approximation,

f of z minus f of alpha almost equals f super prime of alpha times left parenthesis z minus alpha right parenthesis full stop

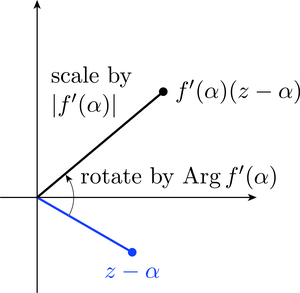
Multiplication of z minus alpha by f super prime of alpha has the effect of scaling z minus alpha by the factor absolute value of f super prime of alpha and rotating it about 0 through the angle Arg of f super prime of alpha; see Figure 6. We refer to f super prime of alpha as a complex scale factor, because it causes both a scaling and a rotation.

Described image
Figure 6 Scaling and rotating z minus alpha
Show description|Hide description

This figure consists of a diagram of the complex plane, focused on the right half-plane. The axes are not labelled. A line segment extends from the origin to a point in the lower-right quadrant. The point is marked with a solid dot and labelled z minus alpha. A second line segment extends from the origin to a point in the upper-right quadrant. The second line segment is longer than the first. Above it is the text, scale by the modulus of f prime of alpha. The point at the end of the second line segment is marked with a solid dot and labelled f prime of alpha times open bracket, z minus alpha, close bracket. A curved arrow between the two line segments points in the anticlockwise direction. Next to it is the text, rotate by Arg f prime of alpha.

Figure 6 Scaling and rotating z minus alpha

We can rewrite the equation above as

f of z almost equals f of alpha plus f super prime of alpha times left parenthesis z minus alpha right parenthesis full stop
Equation label: (equation 2)

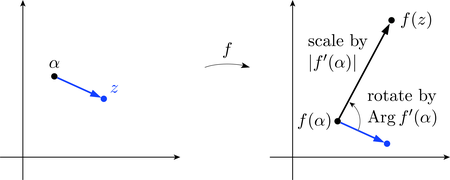
From this we see that f of z is obtained by scaling and rotating the vector z minus alpha based at f of alpha by the complex scale factor f super prime of alpha, as illustrated in Figure 7.

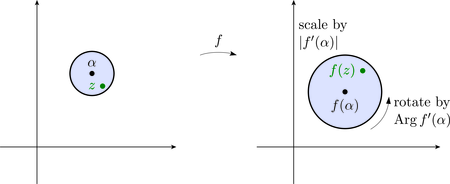
Described image
Figure 7 Interpreting a derivative as a complex scale factor
Show description|Hide description

This figure consists of two copies of the complex plane side by side, both focused on the upper-right quadrant. The axes are not labelled. On the left-hand diagram there are two points in the upper-right quadrant, alpha marked with a solid black dot and z marked with a solid blue dot. The point z lies to the right of the point alpha and a little below it. The vector from alpha to z is drawn as a solid blue line with an arrowhead. Between the left-hand and right-hand diagrams is a curved arrow pointing from left to right and labelled f. On the right-hand diagram, three points are marked with solid dots. The first, which is the closest to the origin, is drawn in black labelled f of alpha. The second, also in black, lies above and to the right of the first point, and is labelled f of z. The third point, drawn in blue, lies to the right and a little below the point labelled f of alpha. It is not labelled. Two vectors are also shown, both starting from the point f of alpha. The first vector, drawn in blue, runs from the point f of alpha to the unlabelled blue point. It is an identical copy of the vector from alpha to z that was drawn in the left-hand diagram. The second vector, drawn in black, starts at the point f of alpha and finishes at the point f of z. Above this second vector is the text, scale by the modulus of f prime of alpha. Between the two vectors is a curved arrow, pointing in the anticlockwise direction. Next to it is the text, rotate by Arg f prime of alpha.

Figure 7 Interpreting a derivative as a complex scale factor

Another useful way to picture how f behaves geometrically is to consider the effect it has on a small disc centred at alpha (still assuming that f super prime of alpha not equals zero). From equation 2 (above), we see that, to a close approximation, a small disc centred at alpha is mapped to a small disc centred at f of alpha. In the process, the disc is rotated through the angle Arg of f super prime of alpha, and it is scaled by the factor absolute value of f super prime of alpha (see Figure 8). As usual, the rotation is anticlockwise if Arg of f super prime of alpha is positive, and clockwise if it is negative.

Described image
Figure 8 The approximate image of a disc centred at a point alpha, where f super prime of alpha not equals zero
Show description|Hide description

This figure consists of two copies of the complex plane side by side, both focused on the upper-right quadrant. The axes are not labelled. On the left-hand diagram a point in the upper-right quadrant is marked with a solid black dot and labelled alpha. A small circular disc is drawn with alpha as its centre and a solid black circle as its boundary. Inside the disc a second point, a little to the right and below the point alpha, is marked with a solid green dot. It is labelled z. The disc is shaded blue. Between the left-hand and right-hand diagrams is a curved arrow pointing from left to right. Above it is the label f. On the right-hand diagram the point f of alpha is marked with a solid black dot and labelled. A circular disc is drawn with the point f of alpha as its centre and a solid black circle as its boundary. This disc has radius approximately 50% greater than the radius of the disc surrounding the point alpha in the left-hand diagram. Inside the disc a second point, above and to the right of the point f of alpha, is marked with a solid green dot and labelled f of z. The disc is shaded blue. Outside the disc, above it and slightly to the left, is the text, scale by the modulus of f prime of alpha. Outside the disc, diametrically opposite the first text, is a curved arrow parallel to the circular boundary of the disc, which points in an anticlockwise direction. Next to it is the text, rotate by Arg f prime of alpha.

Figure 8 The approximate image of a disc centred at a point alpha, where f super prime of alpha not equals zero

The geometric interpretation of derivatives is more complicated if f super prime of alpha equals zero, and we do not discuss it here.

Example 7

Using the notion of a complex scale factor, describe what happens to points close to one plus i under the function f of z equals one solidus z.

Solution

To a close approximation, a small disc centred at one plus i is mapped by f to a small disc centred at

equation sequence part 1 f times left parenthesis one plus i right parenthesis equals part 2 one solidus left parenthesis one plus i right parenthesis equals part 3 one divided by two times left parenthesis one minus i right parenthesis full stop

In the process, the disc is scaled by the factor absolute value of f super prime times left parenthesis one plus i right parenthesis and rotated through the angle Arg of f super prime times left parenthesis one plus i right parenthesis.

Now f super prime of z equals negative one solidus z squared, so

equation sequence part 1 f super prime times left parenthesis one plus i right parenthesis equals part 2 negative one divided by left parenthesis one plus i right parenthesis squared equals part 3 negative one divided by two times i equals part 4 i divided by two comma

which has modulus one solidus two and principal argument pi solidus two.

So f scales the disc by the factor one solidus two and rotates it anticlockwise through the angle pi solidus two.

Exercise 10

Using the notion of a complex scale factor, describe what happens to points close to i under the function

f of z equals four times z plus three divided by two times z squared plus one full stop

Answer

To a close approximation, a small disc centred at i is mapped by f to a small disc centred at

equation sequence part 1 f of i equals part 2 four times i plus three divided by two times i squared plus one equals part 3 negative three minus four times i full stop

In the process the disc is scaled by the factor absolute value of f super prime of i and rotated through the angle Arg of f super prime of i.

By the Quotient Rule,

multiline equation row 1 f super prime of z equals four times left parenthesis two times z squared plus one right parenthesis minus four times z times left parenthesis four times z plus three right parenthesis divided by left parenthesis two times z squared plus one right parenthesis squared row 2 Blank equals negative eight times z squared minus 12 times z plus four divided by left parenthesis two times z squared plus one right parenthesis squared full stop

So

equation sequence part 1 f super prime of i equals part 2 negative eight times i squared minus 12 times i plus four divided by left parenthesis two times i squared plus one right parenthesis squared equals part 3 12 minus 12 times i full stop

This has modulus 12 times Square root of two and principal argument negative pi solidus four.

So f scales the disc by the factor 12 times Square root of two and rotates it clockwise through the angle pi solidus four.

It is important to bear in mind that the complex scale factor interpretation of a derivative is only an approximation, and that it is unlikely to be reliable far from the point under consideration.