Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Introduction to complex analysis
Introduction to complex analysis

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

1.2 Integration on the real line

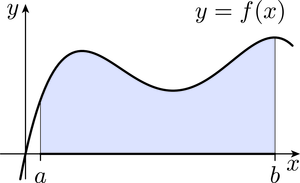
We wish to define the Riemann integral of a continuous real function f in such a way that if f is positive on some interval left square bracket a comma b right square bracket, then the integral of f from a to b is the area under the graph of y equals f of x between a and b. This is illustrated by the shaded part of Figure 8. To do this, we first split the interval left square bracket a comma b right square bracket into a collection of subintervals called a partition.

Described image
Figure 8 Area under the graph of y equals f of x between a and b
Show description|Hide description

The figure shows a set of Cartesian axes labelled x and y concentrated mainly in the upper-right quadrant. The graph of y equals f of x is shown and it passes through the origin from the lower-left quadrant and has two local maximum points and one local minimum. There are points a and b marked on the positive x-axis and joined by a bold line with the point a nearer the origin. Vertical lines join the points a and b to the curve and the area between the graph and the positive x-axis is shaded.

Figure 8 Area under the graph of y equals f of x between a and b

Definitions

A partition cap p of the interval left square bracket a comma b right square bracket is a finite collection of subintervals of left square bracket a comma b right square bracket,

cap p equals left square bracket x sub zero comma x sub one right square bracket comma left square bracket x sub one comma x sub two right square bracket comma ellipsis comma left square bracket x sub n minus one comma x sub n right square bracket comma

for which

multirelation a equals x sub zero less than or equals x sub one less than or equals x sub two less than or equals ellipsis less than or equals x sub n equals b full stop

The length of the subinterval left square bracket x sub k minus one comma x sub k right square bracket is delta times x sub k equals x sub k minus x sub k minus one.

We use absolute value of cap p to denote the maximum length of all the subintervals, so

absolute value of cap p equals max of delta times x sub one comma delta times x sub two comma ellipsis comma delta times x sub n full stop

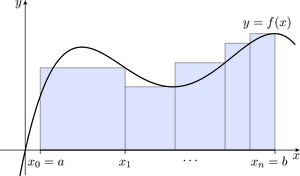
Given a partition cap p equals left square bracket x sub zero comma x sub one right square bracket comma left square bracket x sub one comma x sub two right square bracket comma ellipsis comma left square bracket x sub n minus one comma x sub n right square bracket of left square bracket a comma b right square bracket, we can approximate the area under the graph of y equals f of x between a and b by constructing a sequence of rectangles, as shown in Figure 9.

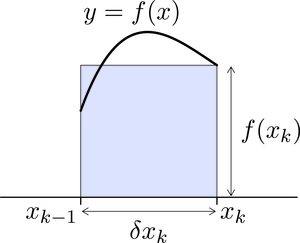
Described image
Figure 9 Approximating the area under a graph using a sequence of rectangles
Show description|Hide description

The figure shows a set of Cartesian axes labelled x and y concentrated mainly in the upper-right quadrant. The graph of y equals f of x is shown which passes through the origin from the lower-left quadrant and has two local maximum points and one local minimum. The points x sub zero equals a is marked on the positive x-axis and is close to the origin. The point x sub one is marked on the positive x-axis and is further from the origin. The point x sub n equals b is marked on the positive x-axis and is further away still. There is an ellipses shown on the positive x-axis to demonstrate the sequence x sub zero to x sub n. There are five consecutive touching rectangles under the curve which have base along the horizontal axis. The base of the first rectangle goes from x sub 0 to x sub1 and its height is from x sub 1 to the curve of y equals f of x. The subsequent four rectangles each have arbitrary width and height which is determined by the right-hand side of the rectangle intersecting the curve. The final rectangle’s right-hand side is at x sub n.

Figure 9 Approximating the area under a graph using a sequence of rectangles

Here the kth rectangle has base left square bracket x sub k minus one comma x sub k right square bracket and height f of x sub k (so the top-right corner of the rectangle touches the curve). The area of the rectangle is f of x sub k times left parenthesis x sub k minus x sub k minus one right parenthesis (see Figure 10). Note that we could equally have chosen the rectangle to be of height f of c sub k for any point c sub k in left square bracket x sub k minus one comma x sub k right square bracket, and the theory would still work. This is because, for a continuous function f, the difference between one set of choices of values for c sub k, k equals one comma two comma ellipsis comma n, and another disappears when we take limits of partitions. We have chosen f of x sub k merely for convenience.

Described image
Figure 10 Rectangle of height f of x sub k and width delta times x sub k
Show description|Hide description

The figure shows a horizontal line with points x sub k minus 1 and point x sub k marked. The distance between the two points is marked with a double-ended arrow as delta x sub k. and creates the base of a shaded rectangle. Part of the curve y equals f of x is shown and a vertical line from the point x sub k meets the curve and this represents the height of the rectangle. The height of the rectangle is labelled with a double-ended arrow as f of x sub k.

Figure 10 Rectangle of height f of x sub k and width delta times x sub k

Summing the areas of all the rectangles gives an approximation to the area under the graph. This sum is called the Riemann sum for f, with respect to this particular partition. (You may have seen upper Riemann sum and lower Riemann sum defined slightly differently elsewhere.)

Definition

The Riemann sum for f with respect to the partition

cap p equals left square bracket x sub zero comma x sub one right square bracket comma left square bracket x sub one comma x sub two right square bracket comma ellipsis comma left square bracket x sub n minus one comma x sub n right square bracket

is the sum

equation sequence part 1 cap r of f comma cap p equals part 2 n ary summation from k equals one to n over f of x sub k times delta times x sub k equals part 3 n ary summation from k equals one to n over f of x sub k times left parenthesis x sub k minus x sub k minus one right parenthesis full stop

We now calculate the Riemann sum for a particular choice of function and partition, and then ask you to do the same for a second function.

Example 1

Let f of x equals x squared, where x element of left square bracket zero comma one right square bracket. Show that for

cap p sub n equals left square bracket zero comma one solidus n right square bracket comma left square bracket one solidus n comma two solidus n right square bracket comma ellipsis comma left square bracket left parenthesis n minus one right parenthesis solidus n comma one right square bracket comma

we have

cap r of f comma cap p sub n equals one divided by six times left parenthesis one plus one solidus n right parenthesis times left parenthesis two plus one solidus n right parenthesis comma

and determine lim over n right arrow normal infinity of cap r of f comma cap p sub n.

Solution

Each of the n subintervals of cap p sub n has length one solidus n. Therefore

multiline equation row 1 cap r of f comma cap p sub n equals n ary summation from k equals one to n over f of k divided by n multiplication one divided by n row 2 Blank equals n ary summation from k equals one to n over left parenthesis k divided by n right parenthesis squared multiplication one divided by n row 3 Blank equals one divided by n cubed times n ary summation from k equals one to n over k squared full stop

Using the identity

equation sequence part 1 n ary summation from k equals one to n over k squared equals part 2 sum with variable number of summands one squared plus two squared plus ellipsis plus n squared equals part 3 one divided by six times n times left parenthesis n plus one right parenthesis times left parenthesis two times n plus one right parenthesis comma

we obtain

equation sequence part 1 cap r of f comma cap p sub n equals part 2 one divided by n cubed multiplication one divided by six times n times left parenthesis n plus one right parenthesis times left parenthesis two times n plus one right parenthesis equals part 3 one divided by six times left parenthesis one plus one solidus n right parenthesis times left parenthesis two plus one solidus n right parenthesis comma

as required.

Finally, since left parenthesis one solidus n right parenthesis is a basic null sequence, we see that

equation sequence part 1 lim over n right arrow normal infinity of cap r of f comma cap p sub n equals part 2 one divided by six times left parenthesis one plus zero right parenthesis times left parenthesis two plus zero right parenthesis equals part 3 one divided by three full stop

Now try the following exercise, making use of the identity

sum with variable number of summands one cubed plus two cubed plus ellipsis plus n cubed equals one divided by four times n squared times left parenthesis n plus one right parenthesis squared full stop

Exercise 1

Let f of x equals x cubed, where x element of left square bracket zero comma one right square bracket. Show that for

cap p sub n equals left square bracket zero comma one solidus n right square bracket comma left square bracket one solidus n comma two solidus n right square bracket comma ellipsis comma left square bracket left parenthesis n minus one right parenthesis solidus n comma one right square bracket comma

we have

cap r of f comma cap p sub n equals one divided by four times left parenthesis one plus one solidus n right parenthesis squared comma

and determine lim over n right arrow normal infinity of cap r of f comma cap p sub n.

Answer

Each of the n subintervals of cap p sub n has length one solidus n. Therefore

multiline equation row 1 cap r of f comma cap p sub n equals n ary summation from k equals one to n over f of k divided by n multiplication one divided by n row 2 Blank equals n ary summation from k equals one to n over left parenthesis k divided by n right parenthesis cubed multiplication one divided by n row 3 Blank equals one divided by n super four times n ary summation from k equals one to n over k cubed row 4 Blank equals one divided by n super four multiplication one divided by four times n squared times left parenthesis n plus one right parenthesis squared row 5 Blank equals one divided by four times left parenthesis one plus one solidus n right parenthesis squared comma

as required.

Since left parenthesis one solidus n right parenthesis is a basic null sequence, we see that

equation sequence part 1 lim over n right arrow normal infinity of cap r of f comma cap p sub n equals part 2 one divided by four times left parenthesis one plus zero right parenthesis squared equals part 3 one divided by four full stop

The Riemann sums cap r of f comma cap p sub n of Example 1 approximate the area under the graph of y equals x squared between zero and one. The approximation improves as n increases, and we expect the limiting value one divided by three to actually be the area under the graph. However, to be sure that this limit gives us a sensible value, we should check that cap r of f comma cap p sub n right arrow one divided by three for any sequence left parenthesis cap p sub n right parenthesis of partitions of left square bracket zero comma one right square bracket such that absolute value of cap p sub n right arrow zero. The following important theorem, for which we omit the proof, provides this check.

Theorem 1

Let f colon left square bracket a comma b right square bracket long right arrow double-struck cap r be a continuous function. Then there is a real number cap a such that

lim over n right arrow normal infinity of cap r of f comma cap p sub n equals cap a comma

for any sequence left parenthesis cap p sub n right parenthesis of partitions of left square bracket a comma b right square bracket such that absolute value of cap p sub n right arrow zero.

We can now define the Riemann integral of a continuous function.

Definition

Let f colon left square bracket a comma b right square bracket long right arrow double-struck cap r be a continuous function, where a less than b. The value cap a determined by Theorem 1 is called the Riemann integral of f over left square bracket a comma b right square bracket, and it is denoted by

integral over a under b f of x d x full stop

The theorem tells us that to calculate the Riemann integral of f over left square bracket a comma b right square bracket, we can make any choice of partitions left parenthesis cap p sub n right parenthesis for which absolute value of cap p sub n right arrow zero and calculate lim over n right arrow normal infinity of cap r of f comma cap p sub n. Thus the calculation of Example 1 really does demonstrate that

integral over zero under one x squared d x equals one divided by three full stop

We define the Riemann integral integral over a under b f of x d x when a greater than or equals b, as follows.

Definitions

Let f be a continuous real function.

If a greater than b, and left square bracket b comma a right square bracket is contained in the domain of f, then we define

integral over a under b f of x d x equals negative integral over b under a f of x d x full stop

Also, for values of a in the domain of f, we define

integral over a under a f of x d x equals zero full stop

As we have discussed, for a continuous real function f that takes only positive values on left square bracket a comma b right square bracket, where a less than b, the Riemann integral

integral over a under b f of x d x

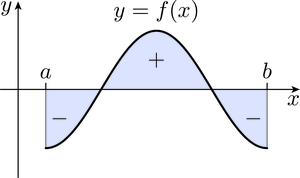
measures the area under the graph of y equals f of x between a and b. If we no longer require f to be positive, then the integral still has a geometric meaning: it measures the signed area of the set between the curve y equals f of x, the x-axis and the vertical lines x equals a and x equals b, where we count parts of the set above the x-axis as having positive area, and parts of the set below the x-axis as having negative area, as illustrated in Figure 11.

Described image
Figure 11 Signed area determined by the graph of y equals f of x between a and b
Show description|Hide description

The figure shows a set of Cartesian axes labelled x and y concentrated in the upper-right and lower-right quadrants. A curve of y equals f of x is labelled. There are points a and b labelled on the positive x-axis with a being nearer the origin. The curve starts in the lower-right quadrant below the positive x-axis directly below the point a, it continues to a local maximum point in the upper-right quadrant and continues to the lower-right quadrant to finish at a point directly below the point b below the positive x-axis. The areas between the curve and the positive x-axis are shaded. The area between the point a and where the curve crosses from the lower-right to the upper-right quadrant is shaded below the positive x-axis and labelled with a minus sign, similarly so too is the area between where the curve crosses back from the upper-right to the lower-right quadrant to the point b. The area above the positive x-axis is shaded and labelled with a plus sign.

Figure 11 Signed area determined by the graph of y equals f of x between a and b