Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Introduction to complex analysis
Introduction to complex analysis

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

1.3 Properties of the Riemann integral

In practice we do not usually calculate integrals by looking at partitions, but instead use a powerful theorem known as the Fundamental Theorem of Calculus, which allows us to think of integration and differentiation as inverse processes.

To state the theorem, we need the notion of a primitive of a continuous real function f colon left square bracket a comma b right square bracket long right arrow double-struck cap r ; this is a real function cap f that is differentiable on left square bracket a comma b right square bracket with derivative equal to f , that is, the function cap f satisfies cap f super prime of x equals f of x , for all x element of left square bracket a comma b right square bracket . A primitive of a function is not unique, because if cap f is a primitive of f , then so is the function with rule cap f of x plus c , for any constant c .

Theorem 2 Fundamental Theorem of Calculus

Let f colon left square bracket a comma b right square bracket long right arrow double-struck cap r be a continuous function. If cap f is a primitive of f , then the Riemann integral of f over left square bracket a comma b right square bracket exists and is given by

integral over a under b f of x d x equals cap f of b minus cap f of a full stop

We denote cap f of b minus cap f of a by left square bracket cap f of x right square bracket sub a super b .

For example, a primitive of f of x equals x squared is cap f of x equals x cubed solidus three , so

equation sequence part 1 integral over zero under one x squared d x equals part 2 left square bracket x cubed divided by three right square bracket sub zero super one equals part 3 one cubed divided by three minus zero cubed divided by three equals part 4 one divided by three comma

which agrees with our earlier calculation using Riemann sums.

The Riemann integral has a number of useful properties.

Theorem 3 Properties of the Riemann integral

Let f and g be real functions that are continuous on the interval left square bracket a comma b right square bracket .

  • a.Sum Rule integral over a under b left parenthesis f of x plus g of x right parenthesis d x equals integral over a under b f of x d x plus integral over a under b g of x d x .

  • b.Multiple Rule integral over a under b lamda times f of x d x equals lamda times integral over a under b f of x d x , for lamda element of double-struck cap r .

  • c.Additivity Rule

    integral over a under b f of x d x equals integral over a under c f of x d x plus integral over c under b f of x d x comma for a less than or equals c less than or equals b full stop

  • d.Substitution Rule If g is differentiable on left square bracket a comma b right square bracket and its derivative g super prime is continuous on left square bracket a comma b right square bracket , and if f is continuous on g of x colon a less than or equals x less than or equals b , then

    integral over a under b f of g of x times g super prime of x d x equals integral over g of a under g of b f of t d t full stop

  • e.Integration by Parts If f and g are differentiable on left square bracket a comma b right square bracket and their derivatives f super prime and g super prime are continuous on left square bracket a comma b right square bracket , then

    integral over a under b f super prime of x times g of x d x equals left square bracket f of x times g of x right square bracket sub a super b minus integral over a under b f of x times g super prime of x d x full stop

  • f.Monotonicity Inequality If f of x less than or equals g of x for each x element of left square bracket a comma b right square bracket , then

    integral over a under b f of x d x less than or equals integral over a under b g of x d x full stop

  • g.Modulus Inequality absolute value of integral over a under b f of x d x less than or equals integral over a under b absolute value of f of x d x .

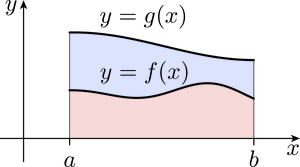
The first five properties are probably familiar to you and we have stated them only for reference. The last two inequalities may be less familiar. The Monotonicity Inequality, illustrated in Figure 12, states that if you replace f by a greater function g , then the integral increases.

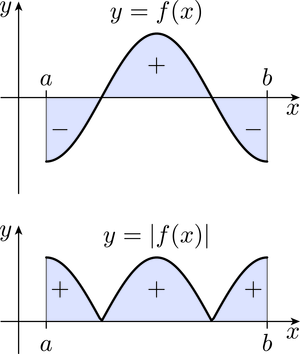
Described image
Figure 12 Monotonicity Inequality
Show description|Hide description

The figure shows a set of Cartesian axes labelled x and y concentrated in the upper-right quadrant. There are points a and b labelled on the positive x-axis with a being nearer the origin. An arbitrary curve labelled y equals g of x slopes down from left to right and another arbitrary curve labelled y equals f of x is below the first curve but this one has a shallow local minimum and maximum. Both curves start and finish at point directly above the points labelled a and b. The area under g of x to f of x is shaded. The area under f of x to the positive x-axis is shaded in a darker shade.

Figure 12 Monotonicity Inequality

The Modulus Inequality, illustrated in Figure 13, says that the modulus of the integral of f over left square bracket a comma b right square bracket (a non-negative number) is less than or equal to the integral of the modulus of f over left square bracket a comma b right square bracket (another non-negative number). If f is positive, then these two numbers are equal, but if f takes negative values, then at least part of the signed area between y equals f of x and the  x -axis is negative, so the first number is less than the second.

Described image
Figure 13 Modulus Inequality
Show description|Hide description

The figure shows two sets of Cartesian axes labelled x and y. The first is concentrated in the upper-right and lower-right quadrants. A curve of y equals f of x is labelled. There are points a and b labelled on the positive x-axis with a being nearer the origin. The curve starts in the lower-right quadrant below the positive x-axis directly below the point a, it continues to a local maximum point in the upper-right quadrant and continues to the lower-right quadrant to finish at a point directly below the point b below the positive x-axis. The areas between the curve and the positive x-axis are shaded. The area between the point a and where the curve crosses from the lower-right to the upper-right quadrant is shaded below the positive x-axis and labelled with a minus sign, similarly so too is the area between where the curve crosses back from the upper-right to the lower-right quadrant to the point b. The area above the positive x-axis is shaded and labelled with a plus sign. The second, which is directly beneath the first, is identical apart from a couple of differences. The curve is labelled y equals modulus f of x. The whole curve is now all above the positive x-axis in the upper-right quadrant and all the shaded areas are labelled with plus signs.

Figure 13 Modulus Inequality

Exercise 2

Use the Monotonicity Inequality and the fact that

e super negative x less than or equals e super negative x squared less than or equals one divided by one plus x squared comma for zero less than or equals x less than or equals one comma

to estimate integral over zero under one e super negative x squared d x from above and below.

Answer

Since

e super negative x less than or equals e super negative x squared less than or equals one divided by one plus x squared comma for zero less than or equals x less than or equals one comma

it follows from the Monotonicity Inequality that

integral over zero under one e super negative x d x less than or equals integral over zero under one e super negative x squared d x less than or equals integral over zero under one one divided by one plus x squared d x full stop

Hence

left square bracket negative e super negative x right square bracket sub zero super one less than or equals integral over zero under one e super negative x squared d x less than or equals left square bracket tangent super negative one of x right square bracket sub zero super one semicolon

that is,

one minus e super negative one less than or equals integral over zero under one e super negative x squared d x less than or equals pi divided by four full stop

Since 0.63 less than one minus e super negative one and pi solidus four less than 0.79 , we see that

0.63 less than integral over zero under one e super negative x squared d x less than 0.79 full stop

(In fact, integral over zero under one e super negative x squared d x equals 0.75 to two decimal places.)