2.2 Integration along a contour
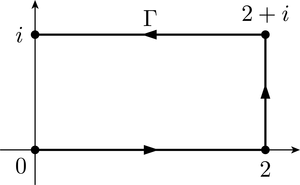
Consider the path from 0 to in Figure 17, with parametrisation given by
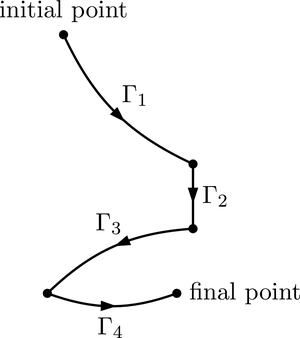
This path is not smooth, because is not differentiable at or . However, can be split into three smooth straight-line paths, joined end to end. This leads to the idea of a contour: it is simply what we get when we place a finite number of smooth paths end to end.
Definitions
A contour is a path that can be subdivided into a finite number of smooth paths joined end to end. The order of these constituent smooth paths is indicated by writing
The initial point of is the initial point of , and the final point of is the final point of .
The definition of a contour is illustrated in Figure 18.
As an example, the contour in Figure 17 can be written as , where , and are smooth paths with smooth parametrisations
Now, we have seen how to integrate a continuous function along a smooth path. It is natural to extend this definition to contours, by splitting the contour into smooth paths and integrating along each in turn. We formalise this idea in the following definition.
Definition
Let be a contour, and let be a function that is continuous on . Then the (contour) integral of along , denoted by , is
Remarks
It is clear that a contour can be split into smooth paths in many different ways. Fortunately, all such splittings lead to the same value for the contour integral. We omit the proof of this result, as it is straightforward but tedious.
When evaluating an integral along a contour , we often consider each smooth path separately, using a convenient parametrisation in each case. For example, consider the contour of Figure 17. To evaluate a contour integral of the form
we can use the smooth parametrisations (above) of , and , or we could use another convenient choice of parametrisations, such as
The alternative notation is sometimes used for contour integrals when the omission of the integration variable will cause no confusion.
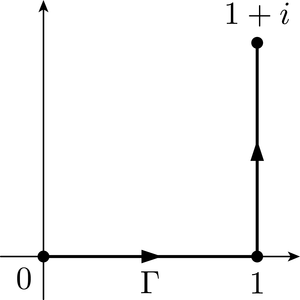
Notice that this answer is the same as that obtained in Example 2 for
where is the line segment from to . The reason for this will become clear when we get to Theorem 8, the Contour Independence Theorem.
Exercise 5
Evaluate
for each of the following contours .
In part (b) the contour consists of a line segment and a semicircle, traversed once anticlockwise. Take to be the initial (and final) point of this contour.
Answer
a., where is the line segment from 0 to 1, is the line segment from 1 to , and is the line segment from to . We choose to use the associated standard parametrisations
Then , , . Hence
b., where is the line segment from to 1, and is the upper half of the circle with centre 0 from 1 to . We choose to use the parametrisations
Then , . Hence
This section will conclude by stating some rules for combining contour integrals. To prove them, we split the contour into constituent smooth paths, and use the Sum Rule and Multiple Rule for real integration given in Theorem 3 to prove the results for each path. We omit the details.
Theorem 5 Combination Rules for Contour Integrals
Let be a contour, and let and be functions that are continuous on .
a.Sum Rule
b.Multiple Rule