Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Introduction to complex analysis
Introduction to complex analysis

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

2.3 Reverse paths and contours

We now introduce the concept of the reverse path (some texts use the name opposite path) of a smooth path normal cap gamma. This is simply the path we obtain by traversing the original path in the opposite direction, starting from the final point of the original path and finishing at the initial point of the original path. In order to define the reverse path formally, we use the fact that as t increases from a to b, so a plus b minus t decreases from b to a.

Definition

Let normal cap gamma colon gamma of t left parenthesis t element of left square bracket a comma b right square bracket right parenthesis be a smooth path. Then the reverse path of normal cap gamma, denoted by cap gamma tilde, is the path with parametrisation gamma tilde, where

gamma tilde of t equals gamma times left parenthesis a plus b minus t right parenthesis times left parenthesis t element of left square bracket a comma b right square bracket right parenthesis full stop

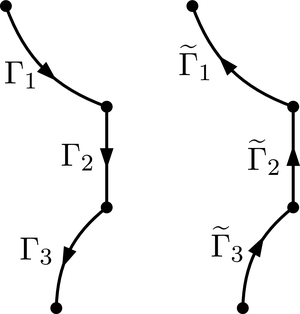
Note that the initial point gamma tilde of a of cap gamma tilde is the final point gamma of b of normal cap gamma, and the final point gamma tilde of b of cap gamma tilde is the initial point gamma of a of normal cap gamma (see Figure 20). The path cap gamma tilde is smooth because normal cap gamma is smooth. Also note that, as sets, normal cap gamma and cap gamma tilde are the same.

Described image
Figure 20 (a) A smooth path normal cap gamma and (b) its reverse path cap gamma tilde
Show description|Hide description

This figure is in two parts: (a) and (b). Part (a) starts with a horizontal line with two points labelled a and b with a being furthest left and a bold line joining the two points. A curved arrow labelled gamma links this to an unlabelled copy of the complex plane concentrated in the upper-right quadrant. A contour labelled capital gamma is labelled and has labelled initial point gamma of a and final point gamma of b. A direction arrow is shown. The contour travels from the point gamma of a near the origin in a left to right and upwards direction to gamma of b. Part (b) again starts with a horizontal line with two points labelled a and b with a being furthest left and a bold line joining the two points. A curved arrow labelled gamma tilde links this to an unlabelled copy of the complex plane concentrated in the upper-right quadrant. A contour labelled capital gamma tilde is labelled and has labelled initial point gamma tilde of a and final point gamma tilde of b and gamma tilde of b is closest to the origin. A direction arrow is shown. The contour travels from point gamma tilde of a to gamma tilde of b right to left and downwards direction.

Figure 20 (a) A smooth path normal cap gamma and (b) its reverse path cap gamma tilde

Exercise 6

Write down the reverse path of the path normal cap gamma with parametrisation

gamma of t equals two plus i minus t times left parenthesis t element of left square bracket zero comma two right square bracket right parenthesis full stop

Answer

Since a equals zero and b equals two, the reverse path is cap gamma tilde colon gamma tilde of t (t element of left square bracket zero comma two right square bracket), where

multiline equation row 1 gamma tilde of t equals gamma times left parenthesis two minus t right parenthesis row 2 Blank equals two plus i minus left parenthesis two minus t right parenthesis row 3 Blank equals t plus i times left parenthesis t element of left square bracket zero comma two right square bracket right parenthesis full stop

We can also define a reverse contour. This is done in the natural way – namely by reversing each of the constituent smooth paths of a contour and reversing the order in which they are traversed.

Definition

Let normal cap gamma equals sum with variable number of summands normal cap gamma sub one plus normal cap gamma sub two plus ellipsis plus normal cap gamma sub n be a contour. The reverse contour cap gamma tilde of normal cap gamma is

cap gamma tilde equals sum with variable number of summands cap gamma tilde sub n plus cap gamma tilde sub n minus one plus ellipsis plus cap gamma tilde sub one full stop

A contour and its reverse contour are illustrated in Figure 21.

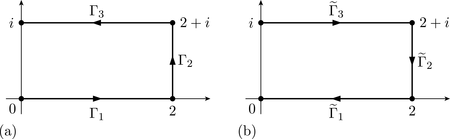
Described image
Figure 21 A contour sum with 3 summands normal cap gamma sub one plus normal cap gamma sub two plus normal cap gamma sub three and its reverse contour sum with 3 summands cap gamma tilde sub three plus cap gamma tilde sub two plus cap gamma tilde sub one
Show description|Hide description

This figure shows two contours side by side, the one on the left is made up of three paths labelled capital gamma sub 1, capital gamma sub 2 and capital gamma sub 3. All have arrows marked in direction of travel. Capital gamma sub 1 is an arc travelling left to right top to bottom and looks like the lower left quarter of a circle. Capital gamma sub 2 is a vertical line travelling top to bottom and capital gamma sub 3 is an arc travelling right to left and top to bottom and looks like the top left quarter of a circle. The contour on the left is the reverse of this contour from capital gamma tilde sub 3 to capital gamma tilde sub 1.

Figure 21 A contour sum with 3 summands normal cap gamma sub one plus normal cap gamma sub two plus normal cap gamma sub three and its reverse contour MathJax failure: TeX parse error: Missing close brace

As an example, if normal cap gamma equals sum with 3 summands normal cap gamma sub one plus normal cap gamma sub two plus normal cap gamma sub three is the contour from 0 to i in Figure 22(a), with smooth parametrisations

multiline equation row 1 gamma sub one of t equals t left parenthesis t element of left square bracket zero comma two right square bracket right parenthesis comma row 2 gamma sub two of t equals two plus i times t left parenthesis t element of left square bracket zero comma one right square bracket right parenthesis comma row 3 gamma sub three of t equals two plus i minus t left parenthesis t element of left square bracket zero comma two right square bracket right parenthesis comma

then cap gamma tilde equals sum with 3 summands cap gamma tilde sub three plus cap gamma tilde sub two plus cap gamma tilde sub one is the contour from i to 0 in Figure 22(b), with smooth parametrisations

multiline equation row 1 gamma tilde sub three of t equals t plus i left parenthesis t element of left square bracket zero comma two right square bracket right parenthesis comma row 2 gamma tilde sub two of t equals two plus i times left parenthesis one minus t right parenthesis left parenthesis t element of left square bracket zero comma one right square bracket right parenthesis comma row 3 gamma tilde sub one of t equals two minus t left parenthesis t element of left square bracket zero comma two right square bracket right parenthesis full stop
Described image
Figure 22 (a) The contour normal cap gamma equals sum with 3 summands normal cap gamma sub one plus normal cap gamma sub two plus normal cap gamma sub three (b) The reverse contour cap gamma tilde equals sum with 3 summands cap gamma tilde sub three plus cap gamma tilde sub two plus cap gamma tilde sub one
Show description|Hide description

This figure is in two parts: (a) and (b). Each part is a copy of the unlabelled complex plane. Part (a) is concentrated in the upper-right quadrant and shows a contour capital gamma labelled and marked with an arrow in an anticlockwise direction. The contour is made up of three line segments. The first labelled capital gamma sub 1 from zero to the labelled point 2, the second labelled capital gamma sub 2 from the point 2 to the labelled point 2 plus i and the last labelled capital gamma sub 3 from 2 plus i to the labelled point i. Part (b) is identical to the left but it is the reverse contour that is indicated. The contours are labelled with capital gamma tilde.

Figure 22 (a) The contour normal cap gamma equals sum with 3 summands normal cap gamma sub one plus normal cap gamma sub two plus normal cap gamma sub three (b) The reverse contour cap gamma tilde equals cap gamma tilde sub three postfix plus full stop full stop full stop

Example 6

Evaluate

integral over cap gamma tilde z macron d z comma

where cap gamma tilde is the reverse path of the line segment normal cap gamma from zero to one plus i.

Solution

We use the standard parametrisation

gamma of t equals left parenthesis one plus i right parenthesis times t times left parenthesis t element of left square bracket zero comma one right square bracket right parenthesis

of normal cap gamma. For the reverse path cap gamma tilde, the corresponding parametrisation is

equation sequence part 1 gamma tilde of t equals part 2 gamma times left parenthesis one minus t right parenthesis equals part 3 left parenthesis one plus i right parenthesis times left parenthesis one minus t right parenthesis times left parenthesis t element of left square bracket zero comma one right square bracket right parenthesis full stop

Then gamma tilde times super prime times left parenthesis t right parenthesis equals negative left parenthesis one plus i right parenthesis, so we substitute

z equals left parenthesis one plus i right parenthesis times left parenthesis one minus t right parenthesis comma z macron equals left parenthesis one minus i right parenthesis times left parenthesis one minus t right parenthesis and d times z equals negative left parenthesis one plus i right parenthesis times d times t

to give

multiline equation row 1 integral over cap gamma tilde z macron d z equals negative integral over zero under one left parenthesis one minus i right parenthesis times left parenthesis one minus t right parenthesis multiplication left parenthesis one plus i right parenthesis d t row 2 Blank equals negative integral over zero under one two times left parenthesis one minus t right parenthesis d t row 3 Blank equation sequence part 1 equals part 2 negative left square bracket two times t minus t squared right square bracket sub zero super one equals part 3 negative one full stop

In Example 3 we saw that

integral over normal cap gamma z macron d z equals one comma

which is the negative of the value negative one that we obtained in Example 6. This illustrates the general result that if we integrate a function along a reverse contour cap gamma tilde, then the answer is the negative of the integral of the function along normal cap gamma.

Theorem 6 Reverse Contour Theorem

Let normal cap gamma be a contour, and let f be a function that is continuous on normal cap gamma. Then the integral of f along the reverse contour cap gamma tilde of normal cap gamma satisfies

integral over cap gamma tilde f of z d z equals negative integral over normal cap gamma f of z d z full stop

Proof

The proof is in two parts. We first prove the result in the case when normal cap gamma is a smooth path, and then extend the proof to contours.

  • a.Let normal cap gamma colon gamma of t left parenthesis t element of left square bracket a comma b right square bracket right parenthesis be a smooth path. Then the parametrisation of cap gamma tilde is

    gamma tilde of t equals gamma times left parenthesis a plus b minus t right parenthesis times left parenthesis t element of left square bracket a comma b right square bracket right parenthesis full stop

    It follows that gamma tilde times super prime times left parenthesis t right parenthesis equals negative gamma times super prime times left parenthesis a plus b minus t right parenthesis, by the Chain Rule, so

    multiline equation row 1 integral over cap gamma tilde f of z d z equals integral over a under b f of gamma tilde of t times gamma tilde times super prime times left parenthesis t right parenthesis d t row 2 Blank equals integral over a under b f of gamma times left parenthesis a plus b minus t right parenthesis times left parenthesis negative gamma times super prime times left parenthesis a plus b minus t right parenthesis right parenthesis d t row 3 Blank equals integral over b under a f of gamma of s times gamma times super prime times left parenthesis s right parenthesis d s row 4 Blank equals negative integral over normal cap gamma f of z d z comma

    where, in the second-to-last line, we have made the real substitution

    s equals a plus b minus t comma d times s equals negative d times t full stop

  • b.To extend the proof to a general contour normal cap gamma, we argue as follows.

    Let normal cap gamma equals sum with variable number of summands normal cap gamma sub one plus normal cap gamma sub two plus ellipsis plus normal cap gamma sub n, for smooth paths normal cap gamma sub one comma normal cap gamma sub two comma ellipsis comma normal cap gamma sub n. Then

    cap gamma tilde equals sum with variable number of summands cap gamma tilde sub n plus cap gamma tilde sub n minus one plus ellipsis plus cap gamma tilde sub one comma

    and we can apply part (a) to see that

    multiline equation row 1 integral over cap gamma tilde f equals integral over cap gamma tilde sub n f plus integral over cap gamma tilde sub n minus one f postfix plus times ellipsis plus integral over cap gamma tilde sub one f row 2 Blank equals negative integral over normal cap gamma sub n f minus integral over normal cap gamma sub n minus one f postfix minus times ellipsis minus integral over normal cap gamma sub one f row 3 Blank equals negative left parenthesis integral over normal cap gamma sub n f plus integral over normal cap gamma sub n minus one f postfix plus times ellipsis plus integral over normal cap gamma sub one f right parenthesis row 4 Blank equals negative integral over normal cap gamma f full stop
∎

In Example 4 we saw that

integral over normal cap gamma one divided by z d z equals two times pi times i comma

where normal cap gamma is the unit circle z colon absolute value of z equals one. The next exercise asks you to check Theorem 6 for this contour integral.

Exercise 7

Verify that

integral over cap gamma tilde one divided by z d z equals negative two times pi times i comma

where normal cap gamma is the unit circle.

Answer

In Example 4 we used the parametrisation

gamma of t equals e super i times t times left parenthesis t element of left square bracket zero comma two times pi right square bracket right parenthesis full stop

For the reverse path cap gamma tilde we use the parametrisation

equation sequence part 1 gamma tilde of t equals part 2 gamma times left parenthesis two times pi minus t right parenthesis equals part 3 e super i times left parenthesis two times pi minus t right parenthesis times left parenthesis t element of left square bracket zero comma two times pi right square bracket right parenthesis full stop

Since e super two times pi times i equals one, we have

gamma tilde of t equals e super negative i times t times left parenthesis t element of left square bracket zero comma two times pi right square bracket right parenthesis comma

and gamma tilde times super prime times left parenthesis t right parenthesis equals negative i times e super negative i times t. Hence

multiline equation row 1 integral over cap gamma tilde one divided by z d z equals integral over zero under two times pi one divided by e super negative i times t multiplication left parenthesis negative i times e super negative i times t right parenthesis d t row 2 Blank equals negative i times integral over zero under two times pi one d t row 3 Blank equals negative two times pi times i full stop

(Therefore, by Example 4,

integral over cap gamma tilde one divided by z d z equals negative integral over normal cap gamma one divided by z d z full stop right parenthesis