3.1 The Fundamental Theorem of Calculus
In Example 5 we saw that
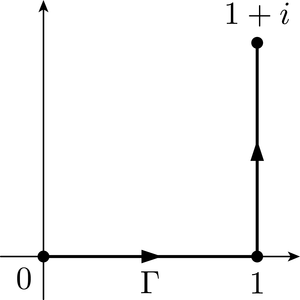
where is the contour shown in Figure 23. Our method was to write down a smooth parametrisation for each of the two line segments, replace in the integral by these parametrisations, and then integrate.
It is, however, tempting to approach this integral as you would a corresponding real integral and write
The Fundamental Theorem of Calculus for contour integrals tells us that this method of evaluation is permissible under certain conditions. Before stating it, we need the idea of a primitive of a complex function, which is defined in a similar way to the primitive of a real function (Section 1.3).
Definition
Let and be functions defined on a region . Then is a primitive of on if is analytic on and
The function is also called an antiderivative or indefinite integral of on .
For example, is a primitive of on , since is analytic on and , for all . Another primitive is ; indeed, any function of the form , where , is a primitive of on .
Exercise 10
Write down a primitive of each of the following functions on the given region .
a.
b.
c.
Answer
a.
b.
c.
We now state the Fundamental Theorem of Calculus for contour integrals, which gives us a quick way of evaluating a contour integral of a function with a primitive that we can determine. The theorem will be proved later in this section.
Theorem 7 Fundamental Theorem of Calculus
Let be a function that is continuous and has a primitive on a region , and let be a contour in with initial point and final point . Then
We often use the notation
Some texts write instead of .
For an example of the use of the Fundamental Theorem of Calculus, observe that if , then is continuous on and has a primitive there. Hence, for the contour in Figure 23, we can write
Exercise 11
Use the Fundamental Theorem of Calculus to evaluate
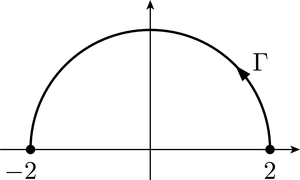
where is the semicircular path shown in Figure 24.
Answer
Let , and . Then is continuous on , and is a primitive of on . Thus, by the Fundamental Theorem of Calculus,
The final simplification follows from the formula
with .
You have seen that
both when is the contour in Figure 23 and also when is the line segment from to (see Example 2). This is not a coincidence: in fact, it is a particular case of the following important consequence of the Fundamental Theorem of Calculus.
Theorem 8 Contour Independence Theorem
Let be a function that is continuous and has a primitive on a region , and let and be contours in with the same initial point and the same final point . Then
Proof
By the Fundamental Theorem of Calculus for contour integrals, the value of each of these integrals is .∎The idea that a contour integral may, under suitable hypotheses, depend only on the endpoints of the contour (and not on the contour itself) has great significance.
Exercise 12
Use the Fundamental Theorem of Calculus to evaluate the following integrals.
a., where is any contour from to .
b., where is any contour from 2 to .
c., where is any contour from to 1.
d., where is any contour from 0 to .
e., where is any contour from 0 to lying in .
Answer
a.Let , and . Then is continuous on , and is a primitive of on . Thus, by the Fundamental Theorem of Calculus,
b.Let , and . Then is continuous on , and is a primitive of on . Thus, by the Fundamental Theorem of Calculus,
c.Let , and . Then is continuous on , and is a primitive of on . Thus, by the Fundamental Theorem of Calculus,
d.The integrand can be written as
which equals by the Chain Rule. So let , and . Then is continuous on , and is a primitive of on . Thus, by the Fundamental Theorem of Calculus,
Remark: If you have a good deal of experience at differentiating and integrating real and complex functions, then you may have chosen to write down the primitive of straight away.
e.The integrand can be written as
which equals
So let
Then is continuous on , and is a primitive of on . Thus, by the Fundamental Theorem of Calculus,
(In this solution, note that the region does not contain the point , as ; thus cannot be chosen to be a path that contains . In particular, the real integral does not exist.)
Next we give a version of Integration by Parts for contour integrals.
Theorem 9 Integration by Parts
Let and be functions that are analytic on a region , and suppose that and are continuous on . Let be a contour in with initial point and final point . Then
Proof
Let and . Then is continuous on , by hypothesis. Also, has primitive , since is analytic on andby the Product Rule for differentiation. It follows from the Fundamental Theorem of Calculus that
that is,
Using the Sum Rule (Theorem 5(a)) and rearranging the resulting equation, we obtain
Example 7
Use Integration by Parts to evaluate
where is any contour from to .
Solution
We take , and . Then and are analytic on , and and are continuous on .
Integrating by parts, we obtain
Exercise 13
Use Integration by Parts to evaluate the following integrals.
a. where is any contour from 0 to .
b., where is any contour from 1 to lying in the cut plane .
(Hint: For part (b), take and .)
Answer
a.We take , and .
Then and are analytic on , and and are continuous on .
Integrating by parts, we obtain
b.We take , and . Then and are analytic on , and and are continuous on .
Integrating by parts, we obtain
The Fundamental Theorem of Calculus is a useful tool when the function being integrated has an easily determined primitive . However, if the function has no primitive, or if we are unable to find one, then we have to resort to the definition of an integral and use parametrisation. For example, we cannot use the Fundamental Theorem of Calculus to evaluate
along any contour, since the function has no primitive on any region.
To see why this is so, suppose that is a function that is defined on a region in the complex plane. We observe that if is not differentiable, then has no primitive . This is because any differentiable complex function can be differentiated as many times as we like. Thus, if has a primitive , then is differentiable with . Hence is also differentiable.
It follows that we cannot use the Fundamental Theorem of Calculus to evaluate integrals of non-differentiable functions such as
We conclude this section by proving the Fundamental Theorem of Calculus.
Proof
The proof of the Fundamental Theorem of Calculus is in two parts. We first prove the result in the case when is a smooth path, and then extend the proof to contours.a.Let be a smooth path. Then
by the Chain Rule. Now, if we write as a sum of its real and imaginary parts , then
The Fundamental Theorem of Calculus for real integrals (Theorem 2) tells us that
Hence
since and .
b.To extend the proof to a general contour with initial point and final point , we argue as follows.
Let , for smooth paths , and let the initial and final points of be and , for . Then
By part (a),
for (where ). Hence