Introduction to complex analysis

Session 1: Differentiation

Introduction to differentiation

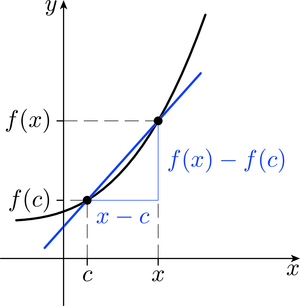
The derivative of a real function at a point is the gradient of the tangent to the graph of at . This gradient is calculated by finding the gradient of the chord joining the point to a (nearby) point , and taking the limit as  approaches (Figure 1).

Figure _unit1.1.1 Figure 1 A chord between two points on a graph

Show description|Hide description

The figure shows Cartesian axes labelled x and y. It is focused on the upper-right quadrant. A smooth curve that looks like part of the graph of a quadratic function with positive coefficient of x-squared starts in the upper-left quadrant a little above the x-axis and a little to the left of the y-axis. At this point it is nearly horizontal. As x increases the curve slopes upwards with steadily increasing gradient. A line with positive gradient also starts in the upper-left quadrant, below the curve, and slopes upwards into the upper-right quadrant. The curve and the line intersect at two points in the upper-right quadrant, both of which are marked with solid dots. The coordinates of these points are illustrated by vertical and horizontal broken line segments joining each point to the x and y axes. From the lower point of intersection, the vertical broken line segment crosses the x-axis at a point marked c. The horizontal broken line segment crosses the y-axis at a point marked f of c. From the upper point of intersection, the vertical broken line segment crosses the x-axis at a point marked x. The horizontal broken line segment crosses the y-axis at a point marked f of x. From the lower point of intersection a horizontal line segment is drawn to the right. It meets a vertical line segment that extends downwards from the upper point of intersection. They form a right-angled triangle with a segment of the original sloping line as its hypotenuse. The length of the horizontal side of this triangle is marked x minus c. The length of its vertical side is marked f of x minus f of c.

Figure 1 A chord between two points on a graph

Now, the gradient of the chord is equal to the ratio

This ratio is often called the difference quotient for at , and its limit as  tends to provides a formal definition of the (real) derivative of at , denoted by . Thus

In the case of complex functions, it is difficult to think about derivatives in terms of gradients of tangents, since the graph of a complex function is not drawn in two dimensions. Instead we define the derivative of a complex function directly in terms of difference quotients, using the notion of complex limits.

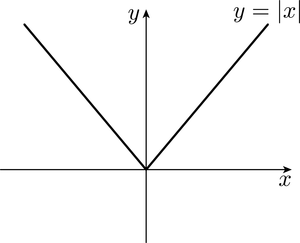
Fortunately, the derivatives of many complex functions turn out to have the same form as those of the corresponding real functions. For example, the derivative of the complex sine function is the complex cosine function, and the complex exponential function is its own derivative. On the other hand, the complex modulus function fails to be differentiable at any point of , even though the real modulus function (Figure 2) is differentiable at every point of . This reflects the fact that complex differentiation imposes a much stronger condition on functions than does real differentiation. Indeed, as the course progresses, you will see that differentiable complex functions have remarkably pleasant properties. For example, if a complex function can be differentiated once throughout a region, then it can be differentiated any number of times. There is no equivalent result for real functions.

Figure _unit1.1.2 Figure 2 Graph of

Show description|Hide description

The figure shows Cartesian axes labelled x and y. It is focused on the upper half-plane. The graph of the function y equals the modulus of x is drawn and labelled. In the upper-left quadrant the graph is a line sloping down with gradient negative 1 to the origin. In the upper-right quadrant the graph is a line sloping up with gradient 1 from the origin.

Figure 2 Graph of

Section 1 will define complex differentiation and show how the definition can be used to establish whether a function is differentiable. By introducing rules for combining differentiable functions, you will see how complex polynomial and rational functions can be differentiated just as in the real case. The end of Section 1 will give a geometric interpretation of complex differentiation by introducing the idea of a complex scale factor.

Section 2 will introduce the concept of partial differentiation for real functions of two real variables, and use it to establish a relationship between complex differentiation and real differentiation. This relationship sometimes enables us to differentiate a complex function using real derivatives. Indeed, at the end of the section, this approach will be used to show that the complex exponential function is its own derivative.