1.2 Circles and triangles
There are many shapes in everyday life: rectangular windows, triangular roof sections and circular ponds. It is these types of more familiar shapes that will be the focus of this section.
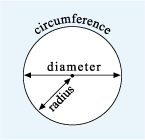
Let’s start with circles, since there is only one type of circle! A circle possesses the property that any point on the circle is always the same distance from the centre point. This distance is known as the radius of the circle. The diameter of a circle is the distance from one edge of the circle to the other, passing through the centre. Finally, the edge of the circle (or the length of this edge) is known as the circumference. You can see all these properties of a circle in Figure 3.
As shown in Figure 3:
Of course, you also know that a circle has 360º.
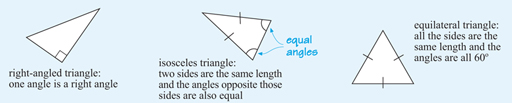
Moving on now to think about triangles. These present us with more to consider, as there are several different standard forms that a triangle can take. Some of these, the right-angled triangle, isosceles triangle and equilateral triangle, are shown in Figure 4. Note that sides that are the same length are marked with the same symbol, usually a short line, perpendicular, to the side.
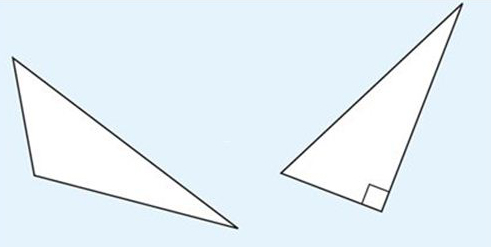
A triangle in which all the sides have different lengths is known as a scalene triangle. Some examples are shown below. You will see that a right-angled triangle can also be described as a scalene triangle, as all the sides are different lengths.
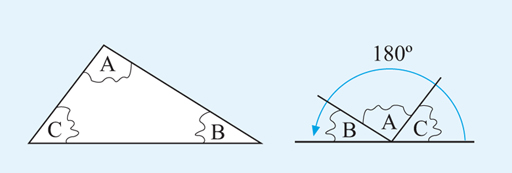
Another important fact is that the angles of a triangle always add up to 180º. To illustrate this, if you cut out any triangle and then tear off the angles, you will be able to arrange them to form a straight line as shown in Figure 6. You might like to try this yourself.
The next section moves to four-sided shapes.