Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Succeed with maths: part 2
Succeed with maths: part 2

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

3.2 Finding an area using formulas

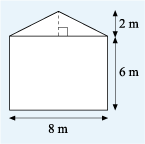
Figure 23 is a rough sketch of the gable end of a house that needs weatherproofing.

A sketch of the gable end of a house
Figure 23 A sketch of the gable end of a house
Show description|Hide description

This is a sketch of the gable end of a house. It is composed of a rectangle of width 8 metres and height 6 metres. An isosceles triangle is placed on the top edge of the rectangle. This triangle has a base of 6 metres and a height of 2 metres.

Figure 23 A sketch of the gable end of a house

To work out the quantity of materials required, the area of the wall is needed. This problem can be broken down by splitting the area into a rectangle and a triangle, then working out these areas and finally adding the two areas together to get the total.

multiline equation line 1 Area of rectanguluar part equals length multiplication width line 2 equals eight m prefix multiplication of six m line 3 equals 48 m super two

The triangle has a base of length 8 m and a perpendicular height of 2 m. So, the area can be calculated as follows:

multiline equation line 1 Area of triangular part equals one divided by two multiplication base multiplication height line 2 equation left hand side equals right hand side one divided by two multiplication eight m prefix multiplication of two m line 3 equals eight m super two

That means the total area of the gable end = 48 m2 + 8 m2.

Now, it’s your turn to put what you’ve learned in this section to use.

Activity 6 Using formulas to calculate areas

Timing: Allow approximately 5 minutes

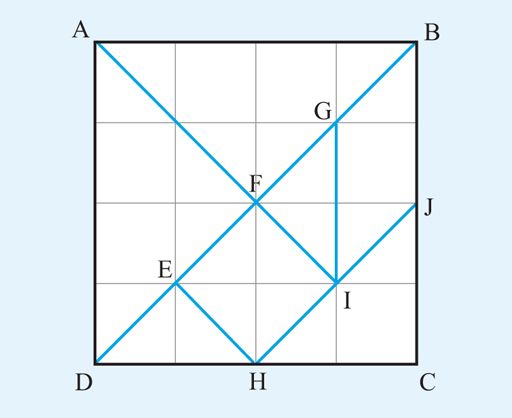
Figure 24 shows the same diagram as you have already seen in previous activities. This time though, instead of counting the squares to determine the areas, use the relevant formulas from the previous section. Remember that the whole grid measures 4 cm by 4 cm, and each small square is 1 cm by 1 cm.

A picture of the square tangram puzzle.
Figure 24 Grid
Show description|Hide description

This is a picture of the square tangram puzzle.

Figure 24 Grid

Calculate the areas of the following shapes.

  • a.Triangle ADF with AD as the base

Answer

  • a.The base of the triangle is AD. AD = 4 cm.

    The perpendicular height from F onto AD = 2 cm.

    area of a triangle equals one divided by two multiplication base multiplication height

    multiline equation line 1 So the area of triangle ADF equals one divided by two multiplication four cm prefix multiplication of two cm line 2 equals four cm super two

  • b.Parallelogram GBJI with BJ as the base

Answer

  • b.BJ = 2 cm. The perpendicular height from G onto BJ = 1 cm.

    Area of a parallelogram equals base multiplication height

    multiline equation line 1 That means the area of GBJI equals two cm prefix multiplication of one cm line 2 equals two cm super two

Now that you know how to calculate the areas of basic shapes, you can calculate more complicated areas by breaking each shape into basic shapes and adding the individual areas together.

Many area problems can be calculated by using combinations of squares, rectangles and triangles. However, you often need to find circular areas, too. The next section will cover this aspect of areas.