4 Volumes
So far you have considered measuring perimeters and areas. But most things in life are not flat; that is, two-dimensional.
Questions like ‘How much does that hold?’ need you to be able to specify the volume of an object. Extending the ideas you learned earlier you can count how many cubes of a certain size will fit into the space. All the sides of a cube are the same length and its six faces are all square.
Useful cubic measurements to use are the cubic millimetre (written as mm3), the cubic centimetre (written as cm3) and the cubic metre (written as m3).
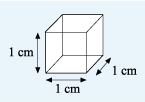
In each case, the length of the side of the cube is 1 unit. So a cubic centimetre has all its sides of length 1 cm, as shown.
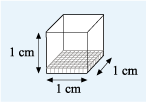
Now imagine filling a cubic centimetre with cubic millimetres. Since there are 10 mm in 1 cm, a cubic centimetre will contain 10 layers with each layer made up of 10 rows, each of 10 cubic millimetres.
So,
Or a 1 cm by 1 cm by 1 cm cube will hold 1000 cubic millimetres.
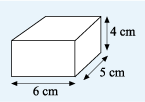
Now, suppose you have a box that measures 6 cm by 5 cm by 4 cm. What is its volume? Since all the dimensions are given in centimetres, you can measure the volume in cubic centimetres. Imagine filling the box with 1 cm3 cubes: six rows with five cubes in each row would cover the bottom of the box, and the box would be filled by four of these layers.
So, the total number of cubes used = 6 x 5 x 4 = 120. The volume of the box is therefore 120 cm3. Before you move on to the next section, can you think of a suitable formula for working out the volume of a rectangular box, known as a cuboid?