3.3.1 How fund managers apply CAPM
For fund managers there is a shorthand way of applying the principles of the CAPM. They can compare the risk of any share or portfolio to that of a benchmark that is represented by the market portfolio. This is achieved using a measure called beta.
Beta measures the sensitivity of returns on a share or portfolio to those of the market (or any other benchmark).
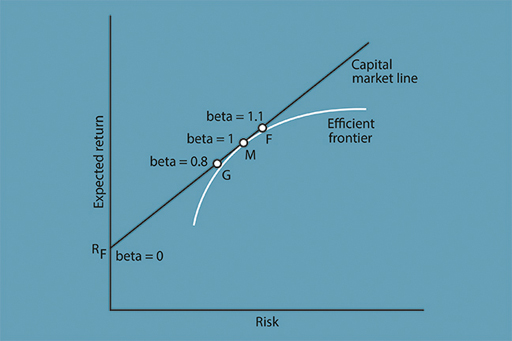
Figure 7 shows how beta is used in a simple example. At the market portfolio M, the value of beta is set equal to 1 by definition. But consider point F, in which beta is equal to 1.1. This portfolio will be more sensitive to market fluctuations than M. It will rise by 11% if the market rises by 10%, and fall by 11% if the market falls by 10%. When its beta is more than 1, a portfolio tends to outperform the market in both directions.
In the risk–return diagram in Figure 7, beta can be adjusted by varying the amount invested in the market portfolio. Consider again what happens if, instead of investing £100 in M, an investor borrows £100 and invests £200: an extra £100 worth of shares added in the same proportion to the portfolio. This will make their portfolio twice as sensitive to the market and so they will have a beta of 2 – taking on twice as much market risk but with twice the expected return. So if the market does well, then they will do very well. Alternatively if, for example, the market falls by 20%, their portfolio is likely to fall by 40%. These are the extreme highs and lows that are associated with leverage (borrowing).
Let’s examine in more detail how borrowing to invest can change your expected return and risk from investing, by considering four different scenarios:
Scenario A: You invest £100 of your money in the market portfolio and the market rises by 5%. You make £5 and your portfolio is now valued at £105.
Scenario B: You invest £200, but only £100 is yours and the other £100 borrowed. The market rises by 5%. You make £10. You repay the £100. So you’re left with £110. A 10% return.
Scenario C: Same as scenario as B but the market falls by 10%. You lose £20 and after repaying the money you are left with £80 – a 20% hit. Without borrowing and investing that extra £100 you would only have taken a hit of £10 (10%).
In Scenario D you borrow £1900 to add to your £100. The market falls by 10% (a hit of £200 on the total portfolio of £2000). So ahead of repaying the lender £1900 you are holding assets worth £1800. Not a good idea!
So gearing-up, by investing with borrowed money, increases the exposure you have to the risk on your portfolio.
Investors who believe in the CAPM and whose portfolios consist only of the market portfolio M and the risk-free asset, are called passive investors. Later this week, you will also be introduced to the Efficient Markets Hypothesis (EMH) that makes the same recommendation. Such investors do not believe that it is possible to consistently outperform the market and so do not try. Next week, you will consider how performance benchmarks can be established that may be tracked by passive investment.
Activity 3.2 Applying CAPM in reality
Look again at Figure 7. Now consider point G at which the beta is equal to 0.8. With a beta of 0.8, what is the likely impact on a portfolio if there is a 10% fall in the market?
Note your answer in the box below.
Answer
The portfolio is expected to fall back by 8%. This is calculated by multiplying 10% by 0.8. When a portfolio’s beta is less than 1, the portfolio will tend to underperform the market in both directions. If at the extreme the portfolio is all held in the risk-free asset, to give a return of Rf, the beta is equal to zero. This portfolio is not at all sensitive to market fluctuations.